
已知角β的终边在直线![]() x-y=0上.
x-y=0上.
(1)写出角β的集合S;
(2)写出S中适合不等式-360°<β<720°的元素.
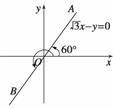 解 (1)如图,直线
解 (1)如图,直线![]() x-y=0过原点,倾斜角为60°,在0°~360°范围内,终边落在射线OA上的角是60°,终边落在射线OB上的角是240°,所以以射线OA、OB为终边的角的集合为:
x-y=0过原点,倾斜角为60°,在0°~360°范围内,终边落在射线OA上的角是60°,终边落在射线OB上的角是240°,所以以射线OA、OB为终边的角的集合为:
S1={β|β=60°+k·360°,k∈Z},
S2={β|β=240°+k·360°,k∈Z},
所以,角β的集合S=S1∪S2={β|β=60°+k·360°,k∈Z}∪{β|β=60°+180°+k·360°,k∈Z}
={β|β=60°+2k·180°,k∈Z}∪{β|β=60°+(2k+1)·180°,k∈Z}={β|β=60°+n·180°,n∈Z}.
(2)由于-360°<β<720°,即-360°<60°+n·180°<720°,n∈Z.解得-![]() <n<
<n<![]() ,n∈Z,所以n=-2,-1,0,1,2,3.
,n∈Z,所以n=-2,-1,0,1,2,3.
所以S中适合不等式-360°<β<720°的元素为:
60°-2×180°=-300°;60°-1×180°=-120°;
60°+0×180°=60°;60°+1×180°=240°;
60°+2×180°=420°;60°+3×180°=600°.


科目:高中数学 来源: 题型:
| 4π |
| 3 |
cos
| ||
sin
|
| 3 |
| 4 |
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com