
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知2(tanA+tanB)= ![]() .
.
(1)证明:a+b=2c;
(2)求cosC的最小值.
【答案】
(1)
证明:由2(tanA+tanB)= ![]() 得:
得:
![]() ;
;
∴两边同乘以cosAcosB得,2(sinAcosB+cosAsinB)=sinA+sinB;
∴2sin(A+B)=sinA+sinB;
即sinA+sinB=2sinC(1);
根据正弦定理, ![]() ;
;
∴ ![]() ,
, ![]() ,
, ![]() ,带入(1)得:
,带入(1)得: ![]() ;
;
∴a+b=2c;
(2)
解:a+b=2c;
∴(a+b)2=a2+b2+2ab=4c2;
∴a2+b2=4c2﹣2ab,且4c2≥4ab,当且仅当a=b时取等号;
又a,b>0;
∴ ![]() ;
;
∴由余弦定理, ![]() =
= ![]() ;
;
∴cosC的最小值为 ![]()
【解析】(1)由切化弦公式 ![]() ,带入
,带入 ![]() 并整理可得2(sinAcosB+cosAsinB)=sinA+cosB,这样根据两角和的正弦公式即可得到sinA+sinB=2sinC,从而根据正弦定理便可得出a+b=2c;
并整理可得2(sinAcosB+cosAsinB)=sinA+cosB,这样根据两角和的正弦公式即可得到sinA+sinB=2sinC,从而根据正弦定理便可得出a+b=2c;
(2)根据a+b=2c,两边平方便可得出a2+b2+2ab=4c2 , 从而得出a2+b2=4c2﹣2ab,并由不等式a2+b2≥2ab得出c2≥ab,也就得到了 ![]() ,这样由余弦定理便可得出
,这样由余弦定理便可得出 ![]() ,从而得出cosC的范围,进而便可得出cosC的最小值.
,从而得出cosC的范围,进而便可得出cosC的最小值.
考查切化弦公式,两角和的正弦公式,三角形的内角和为π,以及三角函数的诱导公式,正余弦定理,不等式a2+b2≥2ab的应用,不等式的性质.
【考点精析】根据题目的已知条件,利用正弦定理的定义和余弦定理的定义的相关知识可以得到问题的答案,需要掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】给出下列4个判断:
①若f(x)=x2-2ax在[1,+∞)上增函数,则a=1;
②函数f(x)=2x-x2只有两个零点;③函数y=2|x|的最小值是1;
④在同一坐标系中函数y=2x与y=2-x的图象关于y轴对称.
其中正确命题的序号是( )
A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xln x,g(x)=x3+ax2-x+2(a∈R).
(1)如果函数g(x)的单调递减区间为![]() ,求函数g(x)的解析式;
,求函数g(x)的解析式;
(2)若不等式2f(x)≤![]() +2恒成立,求实数a的取值范围.
+2恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,其中c为常数,且函数f(x)的图象过原点.
,其中c为常数,且函数f(x)的图象过原点.
(1)求c的值,并求证:f(![]() )+f(x)=1;
)+f(x)=1;
(2)判断函数f(x)在(-1,+∞)上的单调性,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=3n2+8n,{bn}是等差数列,且an=bn+bn+1 .
(1)求数列{bn}的通项公式;
(2)令cn= ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的是______(填上所有符合条件的序号)
①y=e-x在R上为增函数
②任取x>0,均有3x>2x
③函数y=f(x)的图象与直线x=a可能有两个交点
④y=2|x|的最小值为1;
⑤与y=3x的图象关于直线y=x对称的函数为y=log3x.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以O为极点,x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ=2(cos θ+sin θ).
(1)求C的直角坐标方程;
(2)直线l: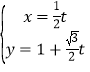 (t为参数)与曲线C交于A,B两点,与y轴交于点E,求|EA|+|EB|.
(t为参数)与曲线C交于A,B两点,与y轴交于点E,求|EA|+|EB|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com