
【题目】已知抛物线C:y2=2x的焦点为F,过焦点F的直线交抛物线于A,B两点,过A,B作准线的垂线交准线与P,Q两点.R是PQ的中点.
(1)证明:以PQ为直径的圆恒过定点F.
(2)证明:AR∥FQ.
【答案】(1)证明见解析(2)证明见解析
【解析】
(1)求得抛物线的焦点F,设直线l的方程为x=my+![]() ,联立抛物线方程,设A(
,联立抛物线方程,设A(![]() ,y1),B(
,y1),B(![]() ,y2),运用韦达定理,求得抛物线的准线方程,可得P,Q,R的坐标,
,y2),运用韦达定理,求得抛物线的准线方程,可得P,Q,R的坐标,
求得![]() ,
,![]() ,由向量垂直的条件,即可得证;
,由向量垂直的条件,即可得证;
(2)设AR的斜率为k1,FQ的斜率为k2,运用直线的斜率公式和两直线平行的条件,以及韦达定理,即可得证.
证明:(1)抛物线C:y2=2x的焦点F(![]() ,0),设直线l的方程为x=my+
,0),设直线l的方程为x=my+![]() ,
,
联立抛物线方程可得y2-2my-1=0,
设A(![]() ,y1),B(
,y1),B(![]() ,y2),则y1+y2=2m,y1y2=-1,
,y2),则y1+y2=2m,y1y2=-1,
抛物线的准线方程为x=-![]() ,可得P(-
,可得P(-![]() ,y1),Q(-
,y1),Q(-![]() ,y2),R(-
,y2),R(-![]() ,
,![]() ),
),
则![]() =(1,-y1),
=(1,-y1),![]() =(1,-y2),可得
=(1,-y2),可得![]()
![]() =1+y1y2=1-1=0,
=1+y1y2=1-1=0,
即PF⊥QF,以PQ为直径的圆恒过定点F;
(2)设AR的斜率为k1,FQ的斜率为k2,
则k2=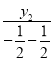 =-y2,
=-y2,
k1=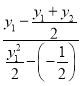 =
=![]() =
=![]() =
=![]() =-y2,
=-y2,
即k1=k2,
则AR∥FQ.


科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,常数
,常数![]() ).
).
(1)当![]() 时,讨论函数
时,讨论函数![]() 的奇偶性并说明理由;
的奇偶性并说明理由;
(2)若函数![]() 在区间
在区间![]() 上单调,求正数
上单调,求正数![]() 的取值范围;
的取值范围;
(3)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为创建全国卫生城市,引入某公司的智能垃圾处理设备.已知每台设备每月固定维护成本![]() 万元,每处理一万吨垃圾需增加
万元,每处理一万吨垃圾需增加![]() 万元维护费用,每月处理垃圾带来的总收益
万元维护费用,每月处理垃圾带来的总收益![]() 万元与每月垃圾处理量
万元与每月垃圾处理量![]() (万吨)满足关系:
(万吨)满足关系: (注:总收益=总成本+利润)
(注:总收益=总成本+利润)
(1)写出每台设备每月处理垃圾获得的利润![]() 关于每月垃圾处理量
关于每月垃圾处理量![]() 的函数关系;
的函数关系;
(2)该市计划引入![]() 台这种设备,当每台每月垃圾处理量为何值时,所获利润最大?并求出最大利润.
台这种设备,当每台每月垃圾处理量为何值时,所获利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,(
,(![]() 为常数)
为常数)
(1)若![]()
①求函数![]() 在区间
在区间![]() 上的最大值及最小值。
上的最大值及最小值。
②若过点![]() 可作函数
可作函数![]() 的三条不同的切线,求实数
的三条不同的切线,求实数![]() 的取值范围。
的取值范围。
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(Ⅰ)根据表中数据,建立![]() 关于的线性回归方程
关于的线性回归方程![]() ;
;
(Ⅱ)根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留小数点后两位)
,计算结果保留小数点后两位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥P﹣ABC中,AC⊥BC,AC=BC=2,PA=PB=PC=3,O是AB中点,E是PB中点.
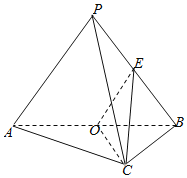
(1)证明:平面PAB⊥平面ABC;
(2)求点B到平面OEC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线方程为![]() ,其中
,其中![]()
(1)求证:直线恒过定点;
(2)当![]() 变化时,求点
变化时,求点![]() 到直线的距离的最大值;
到直线的距离的最大值;
(3)若直线分别与![]() 轴、
轴、![]() 轴的负半轴交于
轴的负半轴交于![]() 两点,求
两点,求![]() 面积的最小值及此时的直线方程.
面积的最小值及此时的直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com