
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.首届中国国际进口博览会的某展馆棚顶一角的钢结构可以抽象为空间图形阳马.如图所示,在阳马![]() 中,
中,![]() 底面
底面![]() .
.

(1)若![]() ,斜梁
,斜梁![]() 与底面
与底面![]() 所成角为
所成角为![]() ,求立柱
,求立柱![]() 的长(精确到
的长(精确到![]() );
);
(2)证明:四面体![]() 为鳖臑;
为鳖臑;
(3)若![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一个动点,求
上一个动点,求![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【解析】
(1)推导出侧棱![]() 在平面
在平面![]() 上的射影是
上的射影是![]() ,从而
,从而![]() 是侧棱
是侧棱![]() 与平面
与平面![]() 所成角,
所成角,![]() ,从而求得立柱
,从而求得立柱![]() 的长.
的长.
(2)四边形![]() 是长方形,从而
是长方形,从而![]() 是直角三角形,由此得出
是直角三角形,由此得出![]() ,从而三角形
,从而三角形![]() 是直角三角形,由
是直角三角形,由![]() 平面
平面![]() ,得
,得![]() 是直角三角形,由此能证明四面体
是直角三角形,由此能证明四面体![]() 为鳖臑.
为鳖臑.
(3)利用转化法求出异面直线![]() 与
与![]() 的距离,即可求得三角形
的距离,即可求得三角形![]() 面积的最小值.
面积的最小值.
(1)因为侧棱![]() 平面
平面![]() ,所以侧棱
,所以侧棱![]() 在底面
在底面![]() 上的射影是
上的射影是![]() ,所以
,所以![]() 是侧棱
是侧棱![]() 与平面
与平面![]() 所成角,所以
所成角,所以![]() ,在
,在![]() 中,
中,![]() ,所以
,所以![]() ,即
,即![]() ,
,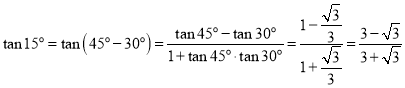 ,所以
,所以![]() .
.
(2)证明:由题意知四边形![]() 是长方形,所以三角形
是长方形,所以三角形![]() 是直角三角形.
是直角三角形.
由于![]() 平面
平面![]() ,所以
,所以![]() ,所以三角形
,所以三角形![]() 和三角形
和三角形![]() 是直角三角形.因为
是直角三角形.因为![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,所以三角形
,所以三角形![]() 是直角三角形.所以四面体
是直角三角形.所以四面体![]() 为鳖臑.
为鳖臑.
(3)![]() 与
与![]() 是两异面直线,
是两异面直线,![]() ,所以
,所以![]() 平面
平面![]() ,则两异面直线
,则两异面直线![]() 与
与![]() 的距离等于
的距离等于![]() 到平面
到平面![]() 的距离,也即
的距离,也即![]() 到平面
到平面![]() 的距离,等于
的距离,等于![]() 到直线
到直线![]() 的距离.因为
的距离.因为![]() ,所以
,所以![]() ,则
,则![]() 到
到![]() 的距离为
的距离为![]() .
.
所以线段![]() 上的动点
上的动点![]() 到
到![]() 的最小距离为
的最小距离为![]() .则三角形
.则三角形![]() 面积的最小值为
面积的最小值为![]() .
.



 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,其长轴、焦距和短轴的长的平方依次成等差数列
,其长轴、焦距和短轴的长的平方依次成等差数列![]() 直线l与x轴正半轴和y轴分别交于点Q、P,与椭圆分别交于点M、N,各点均不重合且满足
直线l与x轴正半轴和y轴分别交于点Q、P,与椭圆分别交于点M、N,各点均不重合且满足![]() .
.
![]() 求椭圆的标准方程;
求椭圆的标准方程;
![]() 若
若![]() ,试证明:直线l过定点并求此定点.
,试证明:直线l过定点并求此定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1:![]() y2=1的左右顶点是双曲线C2:
y2=1的左右顶点是双曲线C2:![]() 的顶点,且椭圆C1的上顶点到双曲线C2的渐近线的距离为
的顶点,且椭圆C1的上顶点到双曲线C2的渐近线的距离为![]() .
.
(1)求双曲线C2的方程;
(2)若直线与C1相交于M1,M2两点,与C2相交于Q1,Q2两点,且![]()
![]() 5,求|M1M2|的取值范围.
5,求|M1M2|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(一),在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置得到图(二),点
的位置得到图(二),点![]() 为棱
为棱![]() 上的动点.
上的动点.

(1)当![]() 在何处时,平面
在何处时,平面![]() 平面
平面![]() ,并证明;
,并证明;
(2)若![]() ,
,![]() ,证明:点
,证明:点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,并求出该距离.
的距离,并求出该距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O经过椭圆C:![]() =1(a>b>0)的两个焦点以及两个顶点,且点(b,
=1(a>b>0)的两个焦点以及两个顶点,且点(b,![]() )在椭圆C上.
)在椭圆C上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l与圆O相切,与椭圆C交于M、N两点,且|MN|=![]() ,求直线l的倾斜角.
,求直线l的倾斜角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com