
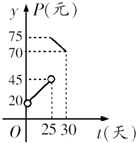
 某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系用下图的两条线段表示;该商品在30天内日销售量Q(件)与时间t(天)之间的关系Q=-t+40.
某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系用下图的两条线段表示;该商品在30天内日销售量Q(件)与时间t(天)之间的关系Q=-t+40.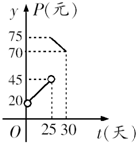 解:(Ⅰ)当0<t<25时,设P=kt+b,则
解:(Ⅰ)当0<t<25时,设P=kt+b,则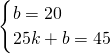
 ∴y=t+20(2分)
∴y=t+20(2分)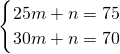 ,∴
,∴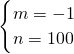 p=-t+100(5分)
p=-t+100(5分)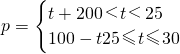 (6分)
(6分)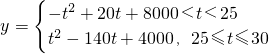 ,利用二次函数的性质进行求解最大值
,利用二次函数的性质进行求解最大值

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
 某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系用如图所示的两条直线段表示:
某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系用如图所示的两条直线段表示:| 第t天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
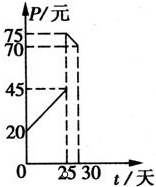 某种商品在30天内每件的销售价格P(元)与时间t(t∈N*)(天)的函数关系用如图的两条线段表示,该商品在30天内日销售量Q(件)与时间t(t∈N*)(天)之间的关系如下表:
某种商品在30天内每件的销售价格P(元)与时间t(t∈N*)(天)的函数关系用如图的两条线段表示,该商品在30天内日销售量Q(件)与时间t(t∈N*)(天)之间的关系如下表:| 第1天 | 5 | 15 | 20 | 30 |
| Q件 | 35 | 25 | 20 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某种商品在30天内每克的销售价格P(元)与时间t的函数图象是如图所示的两条线段AB,CD(不包含A,B两点);该商品在30天内日销售量Q(克)与时间t(天)之间的函数关系如表所示.
某种商品在30天内每克的销售价格P(元)与时间t的函数图象是如图所示的两条线段AB,CD(不包含A,B两点);该商品在30天内日销售量Q(克)与时间t(天)之间的函数关系如表所示.| 第t天 | 5 | 15 | 20 | 30 |
| 销售量Q克 | 35 | 25 | 20 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某种商品在30天内每件销售价格P(元)与时间t(天)的函数关系用如图所示的两条线段表示,该商品在30天内日销售量Q(件)与时间t(天)之间的函数关系是Q=-t+40(0<t≤30,t∈N*).
某种商品在30天内每件销售价格P(元)与时间t(天)的函数关系用如图所示的两条线段表示,该商品在30天内日销售量Q(件)与时间t(天)之间的函数关系是Q=-t+40(0<t≤30,t∈N*).查看答案和解析>>
科目:高中数学 来源: 题型:
 某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系用下图的两条线段表示;该商品在30天内日销售量Q(件)与时间t(天)之间的关系Q=-t+40.
某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系用下图的两条线段表示;该商品在30天内日销售量Q(件)与时间t(天)之间的关系Q=-t+40.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com