练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知数列{an}满足a1＝2，an＋1＝ (n∈N*)，则a3＝________，a1·a2·a3·…·a2007＝________．
    －，3
    (解法1)分别求出a2＝－3、a3＝－、a4＝、a5＝2，可以发现a5＝a1，且a1·a2·a3·a4＝1，故a1·a2·a3·…·a2 007＝a2 005·a2 006·a2 007＝a1·a2·a3＝3.
    (解法2)由an＋1＝，联想到两角和的正切公式，设a1＝2＝tanθ，则有a2＝tan，a3＝tan，a4＝tan，a5＝tan(π＋θ)＝a1，….则a1·a2·a3·a4＝1，
    故a1·a2·a3·…·a2 007＝a2 005·a2 006·a2 007＝a1·a2·a3＝3.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：填空题

    若三角形内切圆的半径为r，三边长为，则三角形的面积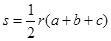，根据类比思想，若四面体内切球半径为R，四个面的面积为S1、S2、S3、S4，则四面体的体积V=                .

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    在平面中，△ABC的角C的内角平分线CE分△ABC面积所成的比.将这个结论类比到空间：在三棱锥A－BCD中，平面DEC平分二面角A－CD－B且与AB交于E，则类比的结论为＝________．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知下列三个方程：x2＋4ax－4a＋3＝0，x2＋(a－1)x＋a2＝0，x2＋2ax－2a＝0，其中至少有一个方程有实根，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    将全体正整数排成一个三角形数阵
    1
    2       3
    4       5      6
    7       8      9      10
    11      12     13     14      15
    …　…　…　…　…　…　…　…　…
    根据以上排列规律，数阵中第行的从左至右的第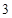个数是              .

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    学习合情推理后，甲、乙两位同学各举了一个例子，
    甲：由“若三角形周长为l，面积为S，则其内切圆半径r＝”类比可得“若三棱锥表面积为S，体积为V，则其内切球半径r＝”；
    乙：由“若直角三角形两直角边长分别为a、b，则其外接圆半径r＝”类比可得“若三棱锥三条侧棱两两垂直，侧棱长分别为a、b、c，则其外接球半径r＝”．这两位同学类比得出的结论(  )
    A．两人都对B．甲错、乙对
    C．甲对、乙错D．两人都错

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    n个连续自然数按规律排列下表：
    0  3 → 4  7 → 8  11…
    ↓  ↑ ↓   ↑  ↓  ↑
    1 → 2  5 → 6  9 → 10
    根据规律，从2010到2012箭头方向依次为________．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    观察按下列顺序排列的等式：，……，猜想第（）个等式应为_         _.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    在计算“1×2+2×3+...+n（n+1）”时，某同学学到了如下一种方法：
    先改写第k项：k（k+1）=
    由此得1×2-.
    .
    .............
    .
    相加，得1×2+2×3+...+n（n+1）.
    类比上述方法，请你计算“1×2×3×4+2×3×4×+....+”，
    其结果是_________________.（结果写出关于的一次因式的积的形式）

    查看答案和解析>>

    同步练习册答案