
分析 (I)由三角形面积公式及余弦定理根据已知可得:2accosB=3×$\frac{1}{2}acsinB$,即可解得tanB的值.
(Ⅱ)将已知等式配方可得(a-1)2+(c-1)2=0,解得a=c=1,经C点向AB作垂线,设垂足为D,可求sinB=$\frac{CD}{CB}$=$\frac{4}{5}$,又BC=1,解得CD,BD,AD,由勾股定理即可求b的值.
解答 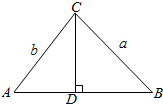 解:(I)∵△ABC的面积为S=$\frac{1}{2}acsinB$,a2+c2=3S+b2,
解:(I)∵△ABC的面积为S=$\frac{1}{2}acsinB$,a2+c2=3S+b2,
又∵由余弦定理可得:a2+c2-b2=2accosB,
∴2accosB=3×$\frac{1}{2}acsinB$,解得:tanB=$\frac{4}{3}$.
(Ⅱ)∵a2+c2+2=2(a+c),
∴a2-2a+1+c2-2c+1=0,
∴(a-1)2+(c-1)2=0,
∴a=c=1,
∵如图,经C点向AB作垂线,设垂足为D,由tanB=$\frac{4}{3}$,可得:cosB=$\sqrt{\frac{1}{1+ta{n}^{2}B}}$=$\frac{3}{5}$,sinB=$\frac{4}{5}$=$\frac{CD}{CB}$,
又∵BC=1,
∴CD=$\frac{4}{5}$,BD=$\frac{3}{5}$,
∴AD=$\frac{2}{5}$,
∴b=AC=$\sqrt{(\frac{4}{5})^{2}+(\frac{2}{5})^{2}}$=$\frac{2\sqrt{5}}{5}$.
点评 本题主要考查了三角形面积公式,余弦定理,勾股定理在解三角形中的应用,考查了转化思想和数形结合思想,属于中档题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{{\sqrt{5}}}{2},2\sqrt{5}}]$ | B. | $({1,\sqrt{5}}]$ | C. | $[{\frac{{\sqrt{5}}}{2},\sqrt{5}}]$ | D. | $[{\sqrt{5},2\sqrt{5}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知A,B是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1左、右顶点,过椭圆中心0作弦MN交椭圆于M,N两点,且$\overrightarrow{AN}$$•\overrightarrow{MN}$=0,|$\overrightarrow{MN}$|=2|$\overrightarrow{AN}$|.
已知A,B是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1左、右顶点,过椭圆中心0作弦MN交椭圆于M,N两点,且$\overrightarrow{AN}$$•\overrightarrow{MN}$=0,|$\overrightarrow{MN}$|=2|$\overrightarrow{AN}$|.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 计算1+3+5+…+2016 | |
| B. | 计算1×3×5×…×2016 | |
| C. | 求方程1×3×5×…×i=2016中的i值 | |
| D. | 求满足1×3×5×…×i>2016中的最小整数i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | $\frac{{\sqrt{7}}}{4}$ | C. | $\frac{5}{3}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
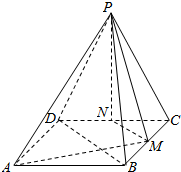 如图,在四棱锥P-ABCD中,侧面PCD丄底面ABCD,△PCD为等边三角形,M为BC中点,N为CD中点.若底面ABCD是矩形且AD=2$\sqrt{2}$,AB=2.
如图,在四棱锥P-ABCD中,侧面PCD丄底面ABCD,△PCD为等边三角形,M为BC中点,N为CD中点.若底面ABCD是矩形且AD=2$\sqrt{2}$,AB=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com