
【题目】已知向量 ![]() =(sin(
=(sin( ![]() x+φ),1),
x+φ),1), ![]() =(1,cos(
=(1,cos( ![]() x+φ))(ω>0,0<φ<
x+φ))(ω>0,0<φ< ![]() ),记函数f(x)=(
),记函数f(x)=( ![]() +
+ ![]() )(
)( ![]() ﹣
﹣ ![]() ).若函数y=f(x)的周期为4,且经过点M(1,
).若函数y=f(x)的周期为4,且经过点M(1, ![]() ).
).
(1)求ω的值;
(2)当﹣1≤x≤1时,求函数f(x)的最值.
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
【题目】已知函数  ,若m<n,且f(m)=f(n),则n﹣m的取值范围是( )
,若m<n,且f(m)=f(n),则n﹣m的取值范围是( )
A.[3﹣2ln2,2)
B.[3﹣2ln2,2]
C.[e﹣1,2]
D.[e﹣1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,建立平面直角坐标系![]() ,
, ![]() 轴在地平面上,
轴在地平面上, ![]() 轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程
轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程![]() 表示的曲线上,其中
表示的曲线上,其中![]() 与发射方向有关.炮的射程是指炮弹落地点的横坐标.
与发射方向有关.炮的射程是指炮弹落地点的横坐标.
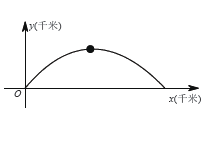
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标![]() 不超过多少时,炮弹可以击中它?请说明理由.
不超过多少时,炮弹可以击中它?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分别求适合下列条件的椭圆的标准方程.
(1)焦点在坐标轴上,且经过点A (![]() ,-2),B(-2
,-2),B(-2![]() ,1);
,1);
(2)与椭圆![]() 有相同焦点且经过点M(
有相同焦点且经过点M(![]() ,1).
,1).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量  ,
, ![]() ,函数
,函数![]() 的图象过点
的图象过点![]() ,点
,点![]() 与其相邻的最高点的距离为
与其相邻的最高点的距离为![]() .
.
(1)求![]() 的单调递增区间;
的单调递增区间;
(2)计算![]() ;
;
(3)设函数![]() ,试讨论函数
,试讨论函数![]() 在区间
在区间![]() 上的零点个数.
上的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在实数集R上定义一种运算“*”,对于任意给定的a、b∈R,a*b为唯一确定的实数,且具有性质:
1)对任意a、b∈R,a*b=b*a;
2)对任意a、b∈R,a*0=a;
3)对任意a、b∈R,(a*b)*c=c*(ab)+(a*c)+(c*b)﹣2c.
关于函数f(x)=x* ![]() 的性质,有如下说法:
的性质,有如下说法:
①在(0,+∞)上函数f(x)的最小值为3;
②函数f(x)为奇函数;
③函数f(x)的单调递增区间为(﹣∞,﹣1),(1,+∞).
其中所有正确说法的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学,给所有同学几何和代数各一题,让各位同学自由选择一道题进行解答.统计情况如下表:(单位:人)
几何题 | 代数题 | 总计 | |
男同学 |
|
|
|
女同学 |
|
|
|
总计 |
|
|
|
(1)能否据此判断有![]() 的把握认为视觉和空间能力与性别有关?
的把握认为视觉和空间能力与性别有关?
(2)经过多次测试发现:女生甲解答一道几何题所用的时间在![]() 分钟,女生乙解答一道几何题所用的时间在
分钟,女生乙解答一道几何题所用的时间在![]() 分钟,现甲、乙两人独立解答同一道几何题,求乙比甲先解答完的概率;
分钟,现甲、乙两人独立解答同一道几何题,求乙比甲先解答完的概率;
(3)现从选择几何题的8名女生中任意抽取两人对她们的答题情况进行研究,记甲、乙两名女生被抽到的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com