
【题目】如表提供了工厂技术改造后某种型号设备的使用年限![]() 和所支出的维修费
和所支出的维修费![]() (万元)的几组对照数据:
(万元)的几组对照数据:
| 2 | 3 | 4 | 5 | 6 |
| 1 | 2.5 | 3 | 4 | 4.5 |
参考公式: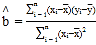 ,
,![]() .
.
(1)若知道![]() 对
对![]() 呈线性相关关系,请根据上表提供的数据,用最小二乘法求出
呈线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该工厂技术改造前该型号设备使用10年的维修费用为9万元,试根据(1)求出的线性回归方程,预测该型号设备技术改造后,使用10年的维修费用能否比技术改造前降低?
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
【题目】2018年是中国改革开放的第40周年,为了充分认识新形势下改革开放的时代性,某地的民调机构随机选取了该地的100名市民进行调查,将他们的年龄分成6段:![]() ,并绘制了如图所示的频率分布直方图.
,并绘制了如图所示的频率分布直方图.

(1)现从年龄在![]() 内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用
内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用![]() 表示年龄在
表示年龄在![]() 内的人数,求
内的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若用样本的频率代替概率,用随机抽样的方法从该地抽取20名市民进行调查,其中有![]() 名市民的年龄在
名市民的年龄在![]() 的概率为
的概率为![]() .当
.当![]() 最大时,求
最大时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时,![]() .现已画出函数
.现已画出函数![]() 在
在![]() 轴右侧的图象,如图所示.
轴右侧的图象,如图所示.
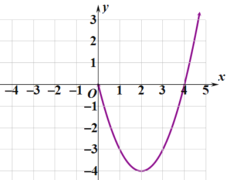
(1)画出函数![]() 在
在![]() 轴左侧的图象,根据图象写出函数
轴左侧的图象,根据图象写出函数![]() 在
在![]() 上的单调区间;
上的单调区间;
(2)求函数![]() 在
在![]() 上的解析式;
上的解析式;
(3)解不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() .
.
(1)如果函数![]() 的单调递减区间为
的单调递减区间为![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)在(1)的条件下,求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(3)若不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知对任意平面向量![]() ,把
,把![]() 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转![]() 角得到向量
角得到向量![]() ,叫做把点
,叫做把点![]() 绕点
绕点![]() 逆时针方向旋转
逆时针方向旋转![]() 角得到点
角得到点![]() .
.
(1)已知平面内点![]() ,点
,点![]() .把点
.把点![]() 绕点
绕点![]() 沿顺时针方向旋转
沿顺时针方向旋转![]() 后得到点
后得到点![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)设平面内曲线![]() 上的每一点绕坐标原点沿逆时针方向旋转
上的每一点绕坐标原点沿逆时针方向旋转![]() 后得到的点的轨迹是曲线
后得到的点的轨迹是曲线![]() ,求原来曲线
,求原来曲线![]() 的方程,并求曲线
的方程,并求曲线![]() 上的点到原点距离的最小值.
上的点到原点距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com