
(本题满分13分)已知y= F(x)的导函数为f(x)=ax3+bx2+cx+d(a≠0),
 函数y=f(x)的图象如右图所示,且函数y=F(x)的图象经过(1,2)和(-1,2)两点,又过点(1,0)作斜率之积为-10的两条直线l1和l2,l1和l2与函数
函数y=f(x)的图象如右图所示,且函数y=F(x)的图象经过(1,2)和(-1,2)两点,又过点(1,0)作斜率之积为-10的两条直线l1和l2,l1和l2与函数![]() 的图象分别相交于A、B两点和C、D两点,O为坐标原点。
的图象分别相交于A、B两点和C、D两点,O为坐标原点。
(1)求函数y=f(x)的对称中心的坐标;
(2)若线段AB和CD的中点分别为M,N,求三角OMN面积的取值范围。
(1)(1,1) (2)![]() ≥
≥![]()
(1)由图像可设y=f(x)=ax(x-1)(x-2)+1
=ax3-3ax2+2ax+1
∵(xn)′=nxn-1(n∈Z),∴F(x)为四次函数,可设F(x)=![]() , 2分
, 2分
又F(1)=2,F(-1)=2, ∴
![]()
![]()
∴f(x)=x3-3x2+2x+1=(x-1)3-x+2
设函数f(x)的图象关于点(m,n)对称,则对任意的x都有f(x)+f(2m-x)=2n,
∴(x-1)3+(2m-x-1)3-2m+4=2n
令x=1与x=m有![]()
![]() 6(m-1)3=0
6(m-1)3=0 ![]() m=1
m=1
∴n=f(m)=f(1)=1 ∴对称中心的坐标为(1,1). 6分
另解:f′(x)=3x2-5x+2,设x1,x2为f′(x)=0的两根,
可知对称中心的横坐标![]() ∴
∴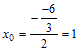 ,
,
∴纵坐标为f(1)=1 ∴对称中心为(1,1) 6分
(2)由(1)可知![]() ,
,
分别设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),M(x5,y5),N(x6,y6).
由题可设l1的方程为y=k(x-1),代入y=x2得x2=kx+l=0,
∴![]() >0
>0 ![]() k>4或k<0 ①
k>4或k<0 ①
l2的方程为![]() ,同理有kx2+10x-10=0 8分
,同理有kx2+10x-10=0 8分
![]() >
>![]() ②
②
由①,②有![]() <k<0或k>4 由上可知
<k<0或k>4 由上可知![]() ,
,![]()
同理 ![]() ,
,![]() ∵
∵![]() <0,∴M,N两点在y轴的两侧.
<0,∴M,N两点在y轴的两侧.
若M点在y轴左侧(如下图所示),则SΔOMN=S梯形MPQN-SΔOQN-SΔOMP
=![]() =
=![]() ,
,
同理当M点在y轴的右侧时,![]()
∴![]() , 11分
, 11分
令![]() ,由双勾函数的性质可知,在
,由双勾函数的性质可知,在![]() <k<0或k>4时,
<k<0或k>4时,
t<![]() 或t≥
或t≥![]() ∴|t|≥
∴|t|≥![]() ∴
∴![]() ≥
≥![]() 13分
13分


科目:高中数学 来源:2012-2013学年湖北省八市高三3月联考理科数学试卷(解析版) 题型:解答题
(本题满分13分)已知△ 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于 .
.
(Ⅰ)求顶点 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 为何种圆锥曲线;
为何种圆锥曲线;
(Ⅱ)当 时,过点
时,过点 的直线
的直线 交曲线
交曲线 于
于 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合) 试问:直线
不重合) 试问:直线 与
与 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届福建省高一上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分13分)已知函数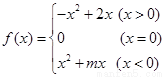 为奇函数;
为奇函数;
(1)求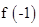 以及m的值;
以及m的值;
(2)在给出的直角坐标系中画出 的图象;
的图象;

(3)若函数 有三个零点,求实数k的取值范围.
有三个零点,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011年湖南省高三第一次学情摸底考试数学卷 题型:解答题
(本题满分13 分)
已知函数
(1)若在 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值;
(2)若 在区间(-2,3)内有两个不同的极值点,求a 取值范围;
在区间(-2,3)内有两个不同的极值点,求a 取值范围;
(3)在(1)的条件下,是否存在实数m,使得函数 的图象与函数
的图象与函数 的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.
的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014届江西省高一第二学期入学考试数学 题型:解答题
.(本题满分13分)已知圆C: 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线
l交圆C于A、B两点.
(1) 当l经过圆心C时,求直线l的方程;
(2) 当弦AB被点P平分时,写出直线l的方程;
(3) 当直线l的倾斜角为45º时,求弦AB的长.
查看答案和解析>>
科目:高中数学 来源:2012届安徽省六校教育研究会高二素质测试理科数学 题型:解答题
(本题满分13分)已知圆C:
(1)若平面上有两点A(1 , 0),B(-1 , 0),点P是圆C上的动点,求使 取得最小值时点P的坐标.
取得最小值时点P的坐标.
(2) 若 是
是 轴上的动点,
轴上的动点, 分别切圆
分别切圆 于
于 两点
两点
①若 ,求直线
,求直线 的方程;
的方程;
②求证:直线 恒过一定点.
恒过一定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com