
【题目】已知椭圆M: ![]() +y2=1,圆C:x2+y2=6﹣a2在第一象限有公共点P,设圆C在点P处的切线斜率为k1 , 椭圆M在点P处的切线斜率为k2 , 则
+y2=1,圆C:x2+y2=6﹣a2在第一象限有公共点P,设圆C在点P处的切线斜率为k1 , 椭圆M在点P处的切线斜率为k2 , 则 ![]() 的取值范围为( )
的取值范围为( )
A.(1,6)
B.(1,5)
C.(3,6)
D.(3,5)
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x﹣a)ex , a∈R. (Ⅰ)当a=1时,试求f(x)的单调增区间;
(Ⅱ)试求f(x)在[1,2]上的最大值;
(Ⅲ)当a=1时,求证:对于x∈[﹣5,+∞), ![]() 恒成立.
恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C:y2=4x,M:(x﹣1)2+y2=4(x≥1),直线l与曲线C相交于A、B两点,O为坐标原点.
(Ⅰ)若 ![]() ,求证:直线l恒过定点,并求出定点坐标;
,求证:直线l恒过定点,并求出定点坐标;
(Ⅱ)若直线l与曲线C1相切,M(1,0),求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线 ![]() 与圆x2+y2=1相交于A、B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( )
与圆x2+y2=1相交于A、B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( )
A.0
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是 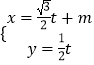 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)设点P(m,0),若直线l与曲线C交于A,B两点,且|PA||PB|=1,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρ=2 ![]() cos(
cos( ![]() ﹣θ)
﹣θ)
(1)求曲线C的直角坐标方程;
(2)已知直线l过点P(1,0)且与曲线C交于A,B两点,若|PA|+|PB|= ![]() ,求直线l的倾斜角α.
,求直线l的倾斜角α.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,且ctanC= ![]() (acosB+bcosA).
(acosB+bcosA).
(1)求角C;
(2)若c=2 ![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学中文系共有本科生5000人,其中一、二、三、四年级的学生比为5:4:3:1,要用分层抽样的方法从该系所有本科生中抽取一个容量为260的样本,则应抽二年级的学生( )
A.100人
B.60人
C.80人
D.20人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=(kx+4)lnx﹣x(x>1),若f(x)>0的解集为(s,t),且(s,t)中只有一个整数,则实数k的取值范围为( )
A.( ![]() ﹣2,
﹣2, ![]() ﹣
﹣ ![]() )
)
B.( ![]() ﹣2,
﹣2, ![]() ﹣
﹣ ![]() ]
]
C.( ![]() ﹣
﹣ ![]() ,
, ![]() ﹣1]
﹣1]
D.( ![]() ﹣
﹣ ![]() ,
, ![]() ﹣1)
﹣1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com