
【题目】已知![]() 的面积为
的面积为![]() ,且满足
,且满足![]() ,则边
,则边![]() 的最小值为_______.
的最小值为_______.
【答案】![]()
【解析】
将正切化成正余弦,化简得出b,c和sinA之间的关系,结合面积公式即可得出b2关于A的函数式,再根据A的范围计算b的最小值,即可得AC的最小值.
∵![]() ,∴
,∴![]() ,∴4cosAsinB+3cosBsinA=sinAsinB,
,∴4cosAsinB+3cosBsinA=sinAsinB,
∴3cosAsinB+3cosBsinA=sinAsinB﹣cosAsinB,
即3sin(A+B)=sinB(sinA﹣cosA),即3sinC=sinB(sinA﹣cosA),
∴3c=b(sinA﹣cosA),即c![]() ,
,
∵△ABC的面积S=![]() bcsinA=
bcsinA=![]()
=![]() (sin2A﹣cosAsinA)=
(sin2A﹣cosAsinA)=![]() (1﹣sin2A﹣cos2A)=
(1﹣sin2A﹣cos2A)=![]() ,
,
∴b2=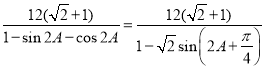 ,∵3c=b(sinA﹣cosA)>0,且0<A<π,
,∵3c=b(sinA﹣cosA)>0,且0<A<π,
∴![]() ,∴当
,∴当![]() 即A=
即A=![]() 时,b2取得最小值
时,b2取得最小值![]() =12,
=12,
∴b的最小值为![]() ,即AC最小值为
,即AC最小值为![]() .
.
故答案为:![]() .
.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:
【题目】南北朝时代的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”. 其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平行平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.如图,夹在两个平行平面之间的两个几何体的体积分别为![]() ,被平行于这两个平面的任意平面截得的两个截面面积分别为
,被平行于这两个平面的任意平面截得的两个截面面积分别为![]() ,则“
,则“![]() 相等”是“
相等”是“![]() 总相等”的
总相等”的

A. 充分而不必要条件B. 必要而不充分条件
C. 充分必要条件D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型商场去年国庆期间累计生成![]() 万张购物单,从中随机抽出
万张购物单,从中随机抽出![]() 张,对每单消费金额进行统计得到下表:
张,对每单消费金额进行统计得到下表:
消费金额(单位:元) |
|
|
|
|
|
购物单张数 | 25 | 25 | 30 | 10 | 10 |
由于工作人员失误,后两栏数据已无法辨识,但当时记录表明,根据由以上数据绘制成的频率分布直方图所估计出的每单消费额的中位数与平均数恰好相等.用频率估计概率,完成下列问题:
(1)估计去年国庆期间该商场累计生成的购物单中,单笔消费额超过![]() 元的概率;
元的概率;
(2)为鼓励顾客消费,该商场打算在今年国庆期间进行促销活动,凡单笔消费超过![]() 元者,可抽奖一次,中一等奖、二等奖、三等奖的顾客可以分别获得价值
元者,可抽奖一次,中一等奖、二等奖、三等奖的顾客可以分别获得价值![]() 元、
元、![]() 元、
元、![]() 元的奖品.已知中奖率为
元的奖品.已知中奖率为![]() ,且一等奖、二等奖、三等奖的中奖率依次构成等比数列,其中一等奖的中奖率为
,且一等奖、二等奖、三等奖的中奖率依次构成等比数列,其中一等奖的中奖率为![]() .若今年国庆期间该商场的购物单数量比去年同期增长
.若今年国庆期间该商场的购物单数量比去年同期增长![]() ,式预测商场今年国庆期间采办奖品的开销.
,式预测商场今年国庆期间采办奖品的开销.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率,数学发展史上出现过多很有创意的求法,如著名的蒲丰试验,受其启发,我们也可以通过设计下面的试验来估计![]() 的值,试验步骤如下:①先请高二年级
的值,试验步骤如下:①先请高二年级![]() 名同学每人在小卡片上随机写下一个实数对
名同学每人在小卡片上随机写下一个实数对![]() ;②若卡片上的
;②若卡片上的![]() ,
,![]() 能与
能与![]() 构成锐角三角形,则将此卡片上交;③统计上交的卡片数,记为
构成锐角三角形,则将此卡片上交;③统计上交的卡片数,记为![]() ;④根据统计数
;④根据统计数![]() ,
,![]() 估计
估计![]() 的值.那么可以估计
的值.那么可以估计![]() 的值约为( )
的值约为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间x与乘客等候人数y之间的关系,经过调查得到如下数据:
间隔时间x/分 | 10 | 11 | 12 | 13 | 14 | 15 |
等候人数y/人 | 23 | 25 | 26 | 29 | 28 | 31 |
调查小组先从这6组数据中选取4组数据求线性回归方程,再用剩下的2组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数y的差,若差值的绝对值都不超过1,则称所求方程是“恰当回归方程”.
与实际等候人数y的差,若差值的绝对值都不超过1,则称所求方程是“恰当回归方程”.
(1)从这6组数据中随机选取4组数据,求剩下的2组数据的间隔时间相邻的概率;
(2)若选取的是中间4组数据,求y关于x的线性回归方程![]() ,并判断此方程是否是“恰当回归方程”.
,并判断此方程是否是“恰当回归方程”.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: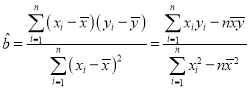 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,离心率
,离心率![]() ,
,![]() 是椭圆的左顶点,
是椭圆的左顶点,![]() 是椭圆的左焦点,
是椭圆的左焦点,![]() ,直线
,直线![]() :
:![]() .
.
(1)求椭圆![]() 方程;
方程;
(2)直线![]() 过点
过点![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,直线
两点,直线![]() 、
、![]() 分别与直线
分别与直线![]() 交于
交于![]() 、
、![]() 两点,试问:以
两点,试问:以![]() 为直径的圆是否过定点,如果是,请求出定点坐标;如果不是,请说明理由.
为直径的圆是否过定点,如果是,请求出定点坐标;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,短轴端点与两焦点围成的三角形面积为
,短轴端点与两焦点围成的三角形面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且过点
两点,且过点![]() ,
,![]() 为坐标原点,当△
为坐标原点,当△![]() 为直角三角形,求直线
为直角三角形,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,菱形![]() 中,
中,![]() ,
,![]() ,
,![]() 于
于![]() .将
.将![]() 沿
沿![]() 翻折到
翻折到![]() ,使
,使![]() ,如图2.
,如图2.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直线A′E与平面A′BC所成角的正弦值;
(Ⅲ)设![]() 为线段
为线段![]() 上一点,若
上一点,若![]() 平面
平面![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的方程为![]() (
(![]() ),其离心率
),其离心率![]() ,
,![]() 分别为椭圆的左、右焦点,
分别为椭圆的左、右焦点,![]() 为椭圆上的点(
为椭圆上的点(![]() 不在
不在![]() 轴上),
轴上),![]() 周长为6.过椭圆右焦点
周长为6.过椭圆右焦点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,
两点,![]() 为坐标原点,
为坐标原点,![]() 面积为
面积为![]() .
.
(1)求椭圆的标准方程:
(2)求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com