【题目】春秋以前中国已有“抱瓮而出灌”的原始提灌方式，使用提水吊杆——桔槔，后发展成辘轳.19世纪末，由于电动机的发明，离心泵得到了广泛应用，为发展机械提水灌溉提供了条件.图形如图所示为灌溉抽水管道在等高图的上垂直投影，在A处测得B处的仰角为37度，在A处测得C处的仰角为45度，在B处测得C处的仰角为53度，A点所在等高线值为20米，若BC管道长为50米，则B点所在等高线值为( )（参考数据
）
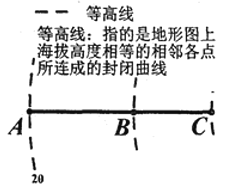
A.30米B.50米C.60米D.70米
暑假作业暑假快乐练西安出版社系列答案科目：高中数学 来源： 题型：
【题目】已知可导函数f（x）的定义域为
，且满足
，
，则对任意的
，“
”是“
”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f（x）在定义域（0，+∞）上是单调函数，且x∈（0，+∞），f（f（x）﹣ex+x）＝e.若不等式2f（x）﹣f′（x）﹣3≥ax对x∈（0，+∞）恒成立，则a的取值范围是（ ）
A.（﹣∞，e﹣2]B.（﹣∞，e﹣1]C.（﹣∞，2e﹣3]D.（﹣∞，2e﹣1]
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中，四边形
是等腰梯形，
，
，
，三角形
是等边三角形，平面
平面，E，F分别为
，
的中点.
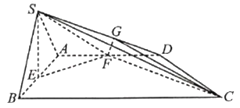
（1）求证：平面
平面
；
（2）若
，求直线
与平面
所成角的正弦值
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若函数
在
处取得极大值或极小值，则称
为函数的极值点．设函数
．
（1）若函数
在
上无极值点，求
的取值范围；
（2）求证：对任意实数，在函数的图象上总存在两条切线相互平行；
（3）当
时，若函数的图象上存在的两条平行切线之间的距离为4，问；这样的平行切线共有几组？请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】春秋以前中国已有“抱瓮而出灌”的原始提灌方式，使用提水吊杆——桔槔，后发展成辘轳.19世纪末，由于电动机的发明，离心泵得到了广泛应用，为发展机械提水灌溉提供了条件.图形如图所示为灌溉抽水管道在等高图的上垂直投影，在A处测得B处的仰角为37度，在A处测得C处的仰角为45度，在B处测得C处的仰角为53度，A点所在等高线值为20米，若BC管道长为50米，则B点所在等高线值为( )（参考数据
）
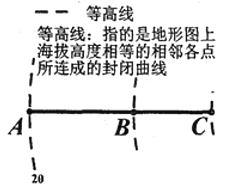
A.30米B.50米C.60米D.70米
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】平面直角坐标系xOy中，抛物线E顶点在坐标原点，焦点为
.以坐标原点为极点，x轴非负半轴为极轴建立极坐标系.
（Ⅰ）求抛物线E的极坐标方程；
（Ⅱ）过点
倾斜角为
的直线l交E于M，N两点，若
，求
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某市数学教研室对全市2018级15000名的高中生的学业水平考试的数学成绩进行调研，随机选取了200名高中生的学业水平考试的数学成绩作为样本进行分析，将结果列成频率分布表如下：
数学成绩 | 频数 | 频率 |
| 5 | 0.025 |
| 15 | 0.075 |
| 50 | 0.25 |
| 70 | 0.35 |
| 45 | 0.225 |
| 15 | 0.075 |
合计 | 200 | 1 |
根据学业水平考试的数学成绩将成绩分为“优秀”、“合格”、“不合格”三个等级，其中成绩大于或等于80分的为“优秀”，成绩小于60分的为“不合格”，其余的成绩为“合格”.
（1）根据频率分布表中的数据，估计全市学业水平考试的数学成绩的众数、中位数（精确到0.1）；
（2）市数学教研员从样本中又随机选取了
名高中生的学业水平考试的数学成绩，如果这
的最小值；
（3）估计全市2018级高中生学业水平考试“不合格”的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
