
【题目】规定:在桌面上,用母球击打目标球,使目标球运动,球的位置是指球心的位置,我们说球 A 是指该球的球心点 A.两球碰撞后,目标球在两球的球心所确定的直线上运动,目标球的运动方向是指目标球被母球击打时,母球球心所指向目标球球心的方向.所有的球都简化为平面上半径为 1 的圆,且母球与目标球有公共点时,目标球就开始运动,在桌面上建立平面直角坐标系,解决下列问题:

(1) 如图,设母球 A 的位置为 (0, 0),目标球 B 的位置为 (4, 0),要使目标球 B 向 C(8, -4) 处运动,求母球 A 球心运动的直线方程;
(2)如图,若母球 A 的位置为 (0, -2),目标球 B 的位置为 (4, 0),能否让母球 A 击打目标 B 球后,使目标 B 球向 (8,-4) 处运动?
(3)若 A 的位置为 (0,a) 时,使得母球 A 击打目标球 B 时,目标球 B(4![]() , 0) 运动方向可以碰到目标球 C(7
, 0) 运动方向可以碰到目标球 C(7![]() ,-5
,-5![]() ),求 a 的最小值(只需要写出结果即可)
),求 a 的最小值(只需要写出结果即可)
【答案】(1)![]() ;(2)不能;(3)
;(2)不能;(3)![]() .
.
【解析】
(1)求出直线![]() 的方程,设出球心的坐标,利用球心在直线
的方程,设出球心的坐标,利用球心在直线![]() 上以及
上以及![]() 列方程组,可求得
列方程组,可求得![]() 的值.,由此求得母球
的值.,由此求得母球![]() 运动的直线方程.(2)计算
运动的直线方程.(2)计算![]() 求得
求得![]() 为锐角,同理
为锐角,同理![]() ,计算点
,计算点![]() 到线段
到线段![]() 的距离,判断出不能.(3)要使
的距离,判断出不能.(3)要使![]() 最小,临界条件为球
最小,临界条件为球![]() 从球
从球![]() 的左上方
的左上方![]() 处撞击球
处撞击球![]() 后,
后,![]() 球从球
球从球![]() 的右上方
的右上方![]() 处撞击球
处撞击球![]() .列方程求得
.列方程求得![]() 的坐标,过
的坐标,过![]() 作倾斜角为
作倾斜角为![]() 的直线,与
的直线,与![]() 轴相交于
轴相交于![]() ,由此求得
,由此求得![]() 的最小值.
的最小值.
(1)
点B(4,0)与点C(8,-4)所石室的直线方程为:x+y-4=0,
依题意,知A,B两球碰撞时,球A的球心在直线x+y-4=0上,且在第一象限,
此时|AB|=2,设A,B两球碰撞时球A的球心坐标为![]() ,
,
则有: ,解得:
,解得:![]() ,
,![]() ,
,
即:A,B两球碰撞时球A的球心坐标为![]() (
(![]() ,
,![]() ),
),
所以,母球A运动的直线方程为:![]()
(2)记![]() ,因为
,因为![]() ,所以
,所以![]() ,故
,故![]() 为锐角,同理可知
为锐角,同理可知![]() 也为锐角.故
也为锐角.故![]() 在直线
在直线![]() 上的投影在线段
上的投影在线段![]() 上,该点到
上,该点到![]() 的距离小于
的距离小于![]() ,故球
,故球![]() 经过该点之前就会与球
经过该点之前就会与球![]() 碰撞,故不可能让母球
碰撞,故不可能让母球![]() 击打目标
击打目标![]() 球后,使目标
球后,使目标![]() 球向
球向![]() 处运动.
处运动.
(3)![]() 的最小值为
的最小值为![]() .要使得
.要使得![]() 最小,临界条件为球
最小,临界条件为球![]() 从球
从球![]() 的左上方
的左上方![]() 处撞击球
处撞击球![]() 后,
后,![]() 球从球
球从球![]() 的右上方
的右上方![]() 处撞击球
处撞击球![]() .如下图所示,设
.如下图所示,设![]() 是球
是球![]() 的所有路径中最远离
的所有路径中最远离![]() 的那条路径上离球
的那条路径上离球![]() 最近的点,则有
最近的点,则有 ,联立
,联立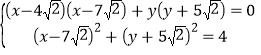 ,解得
,解得![]() ,所有直线
,所有直线![]() 的倾斜角为
的倾斜角为![]() ,所以直线
,所以直线![]() 的倾斜角为
的倾斜角为![]() ,易得
,易得![]() .过
.过![]() 作倾斜角为
作倾斜角为![]() 的直线,交
的直线,交![]() 轴于点
轴于点![]() ,易得
,易得![]() ,就是一个符合题意的初始位置.若
,就是一个符合题意的初始位置.若![]() ,则球
,则球![]() 会在达到
会在达到![]() 之前就与球
之前就与球![]() 碰撞,不合题意.因此
碰撞,不合题意.因此![]() 的最小值为
的最小值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到表格:(单位:人)
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到表格:(单位:人)
经常使用 | 偶尔或不用 | 合计 | |
30岁及以下 | 70 | 30 | 100 |
30岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关?
市使用共享单车情况与年龄有关?
(2)现从所抽取的30岁以上的网友中利用分层抽样的方法再抽取5人.
(i)分别求这5人中经常使用、偶尔或不用共享单车的人数;
(ii)从这5人中,再随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过函数![]() 的图象上的两点
的图象上的两点![]() ,
,![]() 作
作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,
,![]() ,线段
,线段![]() 与函数
与函数![]() 的图象交于点
的图象交于点![]() ,且
,且![]() 与
与![]() 轴平行.
轴平行.

(1)当![]() ,
,![]() ,
,![]() 时,求实数
时,求实数![]() 的值;
的值;
(2)当![]() 时,求
时,求![]() 的最小值;
的最小值;
(3)已知![]() ,
,![]() ,若
,若![]() ,
,![]() 为区间
为区间![]() 内任意两个变量,且
内任意两个变量,且![]() ,
,
求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出,将冰雪这个冷项目迅速炒“热”.北京某综合大学计划在一年级开设冰球课程,为了解学生对冰球运动的兴趣,随机从该校一年级学生中抽取了100人进行调查,其中女生中对冰球运动有兴趣的占![]() ,而男生有10人表示对冰球运动没有兴趣额.
,而男生有10人表示对冰球运动没有兴趣额.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对冰球是否有兴趣与性别有关”?
的把握认为“对冰球是否有兴趣与性别有关”?

(2)若将频率视为概率,现再从该校一年级全体学生中,采用随机抽样的方法每次抽取1名学生,抽取5次,记被抽取的5名学生中对冰球有兴趣的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列,期望和方差.
的分布列,期望和方差.
附表:

![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】王久良导演的纪录片《垃圾围城》真实地反映了城市垃圾污染问题,目前中国668个城市中有超过![]() 的城市处于垃圾的包围之中,且城市垃圾中的快递行业产生的包装垃圾正在逐年攀升,有关数据显示,某城市从2016年到2019年产生的包装垃圾量如下表:
的城市处于垃圾的包围之中,且城市垃圾中的快递行业产生的包装垃圾正在逐年攀升,有关数据显示,某城市从2016年到2019年产生的包装垃圾量如下表:
年份x | 2016 | 2017 | 2018 | 2019 |
包装垃圾y(万吨) | 4 | 6 | 9 | 13.5 |
(1)有下列函数模型:①![]() ;②
;②![]() ;③
;③![]() .
.![]() 试从以上函数模型中,选择模型________(填模型序号),近似反映该城市近几年包装垃圾生产量y(万吨)与年份x的函数关系,并直接写出所选函数模型解析式;
试从以上函数模型中,选择模型________(填模型序号),近似反映该城市近几年包装垃圾生产量y(万吨)与年份x的函数关系,并直接写出所选函数模型解析式;
(2)若不加以控制,任由包装垃圾如此增长下去,从哪年开始,该城市的包装垃圾将超过40万吨?(参考数据:![]()
![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学生小王自主创业,在乡下承包了一块耕地种植某种水果,每季投入2万元,根据以往的经验,每季收获的此种水果能全部售完,且水果的市场价格和这块地上的产量具有随机性,互不影响,具体情况如表:

(Ⅰ)设![]() 表示在这块地种植此水果一季的利润,求
表示在这块地种植此水果一季的利润,求![]() 的分布列及期望;
的分布列及期望;
(Ⅱ)在销售收入超过5万元的情况下,利润超过5万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,离心率为
,离心率为![]() ,
,![]() 为圆
为圆![]() 的圆心.
的圆心.
(1)求椭圆的方程;
(2)已知过椭圆右焦点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,过
两点,过![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且
,且![]() 的解集为
的解集为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意
,对任意![]() ,都有
,都有![]()
(1)求数列![]() 的通项公式.
的通项公式.
(2)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
(3)已知数列![]() ,满足
,满足 ,若
,若 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com