
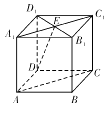
【题目】如图所示,在正方体 ![]() 中,
中, ![]() ,直线
,直线 ![]() 与直线
与直线 ![]() 所成的角为
所成的角为 ![]() ,直线
,直线 ![]() 与平面
与平面 ![]() 所成的角为
所成的角为 ![]() ,则
,则 ![]() ( )
( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】连接BD交AC于O,连接OB1 , 过O作OM⊥BC于M,连接B1M,B1A,B1C.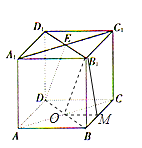
∵B1A=B1C,O是AC的中点,∴OB1⊥AC,
∵B1E平行OB,∴四边形ODEB1是平行四边形,∴OB1∥DE,∴DE⊥AC,∴直线AC与直线DE所成的角为α=90°,
∵OM⊥BC,OM⊥BB1 , ∴OM⊥平面BCC1B1 , ∴∠OB1M为直线DE与平面BCC1B1所成的角β,
∴cos(α-β)=sinβ= ![]() ,∵正方体的棱长AB=2,∴OM=1,OB=
,∵正方体的棱长AB=2,∴OM=1,OB= ![]() BD=
BD= ![]() ∴OB1=
∴OB1=![]() ∴sinβ=
∴sinβ= ![]()
【考点精析】关于本题考查的空间角的异面直线所成的角,需要了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则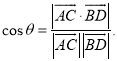 才能得出正确答案.
才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】某商场经营某种商品,在某周内获纯利![]() (元)与该周每天销售这种商品数
(元)与该周每天销售这种商品数![]() 之间的一组数据关系如表:
之间的一组数据关系如表:
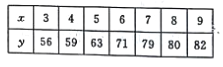
(I)画出散点图;
(II)求纯利![]() 与每天销售件数
与每天销售件数![]() 之间的回归直线方程;
之间的回归直线方程;
(III)估计当每天销售的件数为12件时,每周内获得的纯利为多少?
附注:
![]() ,
,![]() ,
,![]() ,
,![]() ,
, ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题 ![]() “存在
“存在 ![]() ”,命题
”,命题 ![]() :“曲线
:“曲线 ![]() 表示焦点在
表示焦点在 ![]() 轴上的椭圆”,命题
轴上的椭圆”,命题 ![]() “曲线
“曲线 ![]() 表示双曲线”
表示双曲线”
(1)若“ ![]() 且
且 ![]() ”是真命题,求实数
”是真命题,求实数 ![]() 的取值范围;
的取值范围;
(2)若 ![]() 是
是 ![]() 的必要不充分条件,求实数
的必要不充分条件,求实数 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线 ![]() 的焦点为
的焦点为 ![]() ,其准线与
,其准线与 ![]() 轴交于点
轴交于点 ![]() ,过
,过 ![]() 作斜率为
作斜率为 ![]() 的直线
的直线 ![]() 与抛物线交于
与抛物线交于 ![]() 两点,弦
两点,弦 ![]() 的中点为
的中点为 ![]() 的垂直平分线与
的垂直平分线与 ![]() 轴交于
轴交于 ![]() .
.
(1)求 ![]() 的取值范围;
的取值范围;
(2)求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王在年初用50万元购买一辆大货车,第一年因缴纳各种费用需支出6万元,从第二年起,每年都比上一年增加支出2万元,假定该车每年的运输收入均为25万元.小王在该车运输累计收入超过总支出后,考虑将大货车作为二手车出售,若该车在第x年年底出售,其销售价格为25-x万元(国家规定大货车的报废年限为10年).
(1)大货车运输到第几年年底,该车运输累计收入超过总支出?
(2)在第几年年底将大货车出售,能使小王获得的年平均利润最大(利润=累计收入+销售收入-总支出)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足:a1=![]() ,a2=2,3(an+1-2an+an-1)=2.
,a2=2,3(an+1-2an+an-1)=2.
(1)证明:数列{an+1-an}是等差数列;
(2)求使![]() +…+
+…+![]() 成立的最小的正整数n.
成立的最小的正整数n.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com