考点:数列的求和
专题:等差数列与等比数列
分析:(1)由于a
n+1=S
n+1-S
n,可得(S
n+1-S
n)(S
n+1+S
n-2)=2;变形可得(S
n+1-1)
2-(S
n-1)
2=2,且(S
1-1)
2=1,利用等差数列的通项公式即可得出.
(2)①利用S
n=1+
,对n取值即可得出b
3.
②由于2n-1是奇数,S
n=1+
为有理数,可得
=2k-1,可得n=2k
2-2k+1,取k=20,21即可得出.
解答:
解:(1)∵a
n+1=S
n+1-S
n,
∴(S
n+1-S
n)(S
n+1+S
n-2)=2;
即(S
n+1)
2-(S
n)
2-2(S
n+1-S
n)=2,
∴(S
n+1-1)
2-(S
n-1)
2=2,且(S
1-1)
2=1,
∴{(S
n-1)
2}是首项为1,公差为2的等差数列,
∴S
n=1+
.
(2)①n=1时,S
1=1+1=2=b
1,n=5时,S
5=1+3=4=b
2,n=13时,S
13=1+5=6=b
3.
②∵2n-1是奇数,S
n=1+
为有理数,则
=2k-1,
∴n=2k
2-2k+1,
当k=20时,n=761;当k=21时,n=841;
∴存在N∈[761,840],当n≤N时,使得在{S
n}中,数列{b
k}有且只有20项.
点评:本题考查了变形转化为等差数列的方法,考查了等差数列的通项公式、分类讨论的思想方法,考察了推理能力与计算能力,属于难题.



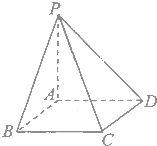 如图,四棱锥P-ABCD的底面ABCD是边长为l的正方形,侧棱PA=1,PB=PD=
如图,四棱锥P-ABCD的底面ABCD是边长为l的正方形,侧棱PA=1,PB=PD=