
【题目】下列函数中,既是偶函数,又在区间(0,+∞)上单调递减的函数是( )
A.y=x2B.![]() C.y=2|x|D.y=cosx
C.y=2|x|D.y=cosx
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】![]() 是双曲线
是双曲线![]() 的左右焦点,过
的左右焦点,过![]() 且斜率为1的直线与两条渐近线分别交于
且斜率为1的直线与两条渐近线分别交于![]() 两点,若
两点,若![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】设直线方程为![]() ,与渐近线方程
,与渐近线方程![]() 联立方程组解得
联立方程组解得![]() 因为
因为![]() ,所以
,所以![]()
![]() ,选B.
,选B.
点睛:解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于![]() 的方程或不等式,再根据
的方程或不等式,再根据![]() 的关系消掉
的关系消掉![]() 得到
得到![]() 的关系式,而建立关于
的关系式,而建立关于![]() 的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.
的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.
【题型】单选题
【结束】
10
【题目】设![]() 是两条不同的直线,
是两条不同的直线, ![]() 是两个不同的平面,则下列命题中正确的是( )
是两个不同的平面,则下列命题中正确的是( )
A. 若![]() ,
, ![]() ,则
,则![]()
B. 若![]() ,
, ![]() ,则
,则![]()
C. 若![]() ,
, ![]() ,
, ![]() ,则
,则![]()
D. 若![]() ,且
,且![]() ,点
,点![]() ,直线
,直线![]() ,则
,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象为C,如下结论中正确的是( )
的图象为C,如下结论中正确的是( )
①图象C关于直线![]() 对称;②函数
对称;②函数![]() 在区间
在区间![]() 内是增函数;
内是增函数;
③图象C关于点![]() 对称;④由
对称;④由![]() 的图象向右平移
的图象向右平移![]() 个单位长度可以得到图象C
个单位长度可以得到图象C
A.①③B.②③C.①②③D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
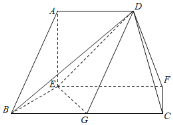
【题目】在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
(Ⅰ)求证:AB∥平面DEG;
(Ⅱ)求二面角C-DF-E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是公差不为零的等差数列,满足
是公差不为零的等差数列,满足![]() ,且
,且![]() 、
、![]() 、
、![]() 成等比数列.
成等比数列.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)设等差数列![]() 的公差为
的公差为![]() ,由a3=7,且
,由a3=7,且![]() 、
、![]() 、
、![]() 成等比数列.可得
成等比数列.可得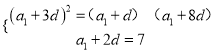 ,解之得即可得出数列
,解之得即可得出数列![]() 的通项公式;
的通项公式;
2)由(1)得![]() ,则
,则![]() ,由裂项相消法可求数列
,由裂项相消法可求数列![]() 的前
的前![]() 项和
项和![]() .
.
试题解析:(1)设数列![]() 的公差为
的公差为![]() ,且
,且![]() 由题意得
由题意得![]() ,
,
即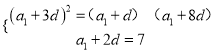 ,解得
,解得![]() ,
,
所以数列![]() 的通项公式
的通项公式![]() .
.
(2)由(1)得![]()
![]() ,
,
![]()
![]() .
.
【题型】解答题
【结束】
18
【题目】四棱锥![]() 的底面
的底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 为正三角形.
为正三角形.
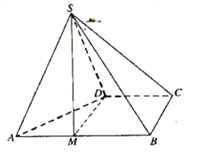
(1)点![]() 为棱
为棱![]() 上一点,若
上一点,若![]() 平面
平面![]() ,
,![]() ,求实数
,求实数![]() 的值;
的值;
(2)求点B到平面SAD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x|(x﹣a),a为实数.
(1)若函数f(x)为奇函数,求实数a的值;
(2)若函数f(x)在[0,2]为增函数,求实数a的取值范围;
(3)是否存在实数a(a<0),使得f(x)在闭区间![]() 上的最大值为2,若存在,求出a的值;若不存在,请说明理由.
上的最大值为2,若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求![]() 的最小正周期;
的最小正周期;
(2)当![]() 时,
时,
(ⅰ)求函数![]() 的单调递减区间;
的单调递减区间;
(ⅱ)求函数![]() 的最大值最小值,并分别求出使该函数取得最大值最小值时的自变量
的最大值最小值,并分别求出使该函数取得最大值最小值时的自变量![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com