
【题目】已知抛物线![]() :
: ![]() (
(![]() )的焦点是椭圆
)的焦点是椭圆![]() :
: ![]() (
(![]() )的右焦点,且两曲线有公共点
)的右焦点,且两曲线有公共点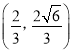
(1)求椭圆![]() 的方程;
的方程;
(2)椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
, ![]() ,若过点
,若过点![]() 且斜率不为零的直线
且斜率不为零的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,已知直线
两点,已知直线![]() 与
与![]() 相较于点
相较于点![]() ,试判断点
,试判断点![]() 是否在一定直线上?若在,请求出定直线的方程;若不在,请说明理由.
是否在一定直线上?若在,请求出定直线的方程;若不在,请说明理由.
【答案】(1) ![]() (2) 点
(2) 点![]() 在定直线
在定直线![]() 上
上
【解析】试题分析:(1)由条件易得: 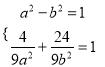 ,从而得到椭圆
,从而得到椭圆![]() 的方程;
的方程;
(2)先由特殊位置定出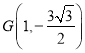 ,猜想点
,猜想点![]() 在直线
在直线![]() 上,由条件可得直线
上,由条件可得直线![]() 的斜率存在, 设直线
的斜率存在, 设直线![]() ,联立方程
,联立方程![]() ,消
,消![]() 得:
得: ![]() 有两个不等的实根,利用韦达定理转化条件即可.
有两个不等的实根,利用韦达定理转化条件即可.
试题解析:
(1)将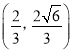 代入抛物线
代入抛物线![]() 得
得![]()
∴抛物线的焦点为![]() ,则椭圆
,则椭圆![]() 中
中![]() ,
,
又点 在椭圆
在椭圆![]() 上,
上,
∴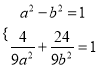 , 解得
, 解得![]() ,
,
椭圆![]() 的方程为
的方程为![]()
(2)方法一
当点![]() 为椭圆的上顶点时,直线img src="http://thumb.zyjl.cn/questionBank/Upload/2018/08/07/18/5075df16/SYS201808071806350814512596_DA/SYS201808071806350814512596_DA.027.png" width="9" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />的方程为
为椭圆的上顶点时,直线img src="http://thumb.zyjl.cn/questionBank/Upload/2018/08/07/18/5075df16/SYS201808071806350814512596_DA/SYS201808071806350814512596_DA.027.png" width="9" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />的方程为![]() ,此时点
,此时点![]() ,
, 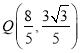 ,则直线
,则直线![]() 和直线
和直线![]() ,联立
,联立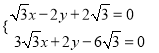 ,解得
,解得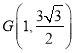 ,
,
当点![]() 为椭圆的下顶点时,由对称性知:
为椭圆的下顶点时,由对称性知: 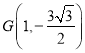 .
.
猜想点![]() 在直线
在直线![]() 上,证明如下:
上,证明如下:
由条件可得直线![]() 的斜率存在, 设直线
的斜率存在, 设直线![]() ,
,
联立方程![]() ,
,
消![]() 得:
得: ![]() 有两个不等的实根,
有两个不等的实根,
![]() ,
, ![]()
设![]() ,则
,则![]() ,
, ![]()
则直线![]() 与直线
与直线![]()
联立两直线方程得![]() (其中
(其中![]() 为
为![]() 点横坐标)
点横坐标)
将![]() 代入上述方程中可得
代入上述方程中可得![]() ,
,
即![]() ,
,
即证![]()
将![]() 代入上式可得
代入上式可得![]()
![]() ,此式成立
,此式成立
∴点![]() 在定直线
在定直线![]() 上.
上.
方法二
由条件可得直线![]() 的斜率存在, 设直线
的斜率存在, 设直线![]()
联立方程![]() ,
,
消![]() 得:
得: ![]() 有两个不等的实根,
有两个不等的实根,
![]() ,
, ![]()
设![]() ,则
,则![]() ,
, ![]()
![]() ,
,
由![]() ,
, ![]() ,
, ![]() 三点共线,有:
三点共线,有: ![]()
由![]() ,
, ![]() ,
, ![]() 三点共线,有:
三点共线,有: ![]()
上两式相比得![]()
![]() ,
,
解得![]()
∴点![]() 在定直线
在定直线![]() 上.
上.


科目:高中数学 来源: 题型:
【题目】已经函数![]() 的定义域为
的定义域为![]() ,设
,设![]()
(1)试确定![]() 的取值范围,使得函数
的取值范围,使得函数![]() 在
在![]() 上为单调函数
上为单调函数
(2)求证![]()
(3)若不等式![]() (为
(为![]() 正整数)对任意正实数
正整数)对任意正实数![]() 恒成立,求
恒成立,求![]() 的最大值.(解答过程可参考使用以下数据
的最大值.(解答过程可参考使用以下数据![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,圆
,圆![]() ,点
,点![]() 是圆上一动点,
是圆上一动点, ![]() 的垂直平分线与线段
的垂直平分线与线段![]() 交于点
交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 且斜率不为0的直线
且斜率不为0的直线![]() 与
与![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明直线
,证明直线![]() 过定点,并求
过定点,并求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 是自然对数的底数)
是自然对数的底数)
(1)若直线![]() 为曲线
为曲线![]() 的一条切线,求实数
的一条切线,求实数![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 上为单调函数,求实数
上为单调函数,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,若
,若![]() 在定义域上有极值点(极值点是指函数取得极值时对应的自变量的值),求实数
在定义域上有极值点(极值点是指函数取得极值时对应的自变量的值),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海产品经销商调查发现,该海产品每售出![]() 吨可获利
吨可获利![]() 万元,每积压
万元,每积压![]() 吨则亏损
吨则亏损![]() 万元.根据往年的数据,得到年需求量的频率分布直方图如图所示,将频率视为概率.
万元.根据往年的数据,得到年需求量的频率分布直方图如图所示,将频率视为概率.
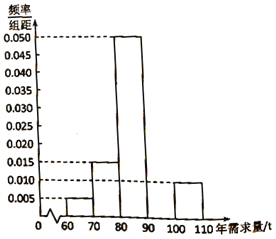
(1)请补齐![]() 上的频率分布直方图,并依据该图估计年需求量的平均数;
上的频率分布直方图,并依据该图估计年需求量的平均数;
(2)今年该经销商欲进货![]() 吨,以
吨,以![]() (单位:吨,
(单位:吨, ![]() )表示今年的年需求量,以
)表示今年的年需求量,以![]() (单位:万元)表示今年销售的利润,试将
(单位:万元)表示今年销售的利润,试将![]() 表示为
表示为![]() 的函数解析式;并求今年的年利润不少于
的函数解析式;并求今年的年利润不少于![]() 万元的概率.
万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,且
,且![]() 与抛物线
与抛物线![]() 的焦点重合.
的焦点重合.
(1)求椭圆的标准方程;
(2)若过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,过
两点,过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,且
两点,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科学技术的飞速发展,手机的功能逐渐强大,很大程度上代替了电脑、电视.为了了解某高校学生平均每天使用手机的时间是否与性别有关,某调查小组随机抽取了![]() 名男生、
名男生、![]() 名女生进行为期一周的跟踪调查,调查结果如表所示:
名女生进行为期一周的跟踪调查,调查结果如表所示:
平均每天使用手机超过 | 平均每天使用手机不超过 | 合计 | |
男生 |
|
|
|
女生 |
|
|
|
合计 |
|
|
|
(1)能否在犯错误的概率不超过![]() 的前提下认为学生使用手机的时间长短与性别有关?
的前提下认为学生使用手机的时间长短与性别有关?
(2)在这![]() 名女生中,调查小组发现共有
名女生中,调查小组发现共有![]() 人使用国产手机,在这
人使用国产手机,在这![]() 人中,平均每天使用手机不超过
人中,平均每天使用手机不超过![]() 小时的共有
小时的共有![]() 人.从平均每天使用手机超过
人.从平均每天使用手机超过![]() 小时的女生中任意选取
小时的女生中任意选取![]() 人,求这
人,求这![]() 人中使用非国产手机的人数
人中使用非国产手机的人数![]() 的分布列和数学期望.
的分布列和数学期望.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: 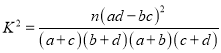
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数的极值;
垂直,求函数的极值;
(2)设函数![]() .当
.当![]() =
=![]() 时,若区间[1,e]上存在x0,使得
时,若区间[1,e]上存在x0,使得![]() ,求实数
,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数底数)
为自然对数底数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com