
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 可由这两圆的极坐标方程,在方程的两边同乘以ρ即可得出其平面直角坐标系下的方程,根据方程可画出这两圆的图形,从而由图形即可求出|AB|的值.
解答 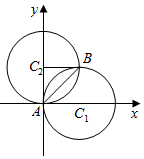 解:由ρ=2cosθ得,ρ2=2ρcosθ;
解:由ρ=2cosθ得,ρ2=2ρcosθ;
∴x2+y2=2x;
∴(x-1)2+y2=1;
∴该圆表示以(1,0)为圆心,1为半径的圆;
由ρ=2sinθ得,ρ2=2ρsinθ;
∴x2+y2=2y;
∴x2+(y-1)2=1;
∴该圆表示以(0,1)为圆心,1为半径的圆;
画出这两个圆的图形如图:
△ABC2为Rt△,C2A=C2B=1;
∴$AB=\sqrt{2}$.
故选B.
点评 考查圆的极坐标方程的表示,以及极坐标和直角坐标互化的公式,以及圆的标准方程,数形结合解题的方法.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,ABCD是正方形,O是该正方形的中心,P是平面 ABCD 外一点,PO⊥底面ABCD,E是PC的中点.
如图,ABCD是正方形,O是该正方形的中心,P是平面 ABCD 外一点,PO⊥底面ABCD,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
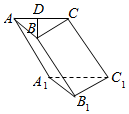 如图:在三棱柱ABC-A1B1C1中,∠A1B1C1=90°,A1B1=B1C1=AA1=2,且C在底面A1B1C1上的射影A1C1边的中点,D为AC的中点,点E在CC1上,且$\overrightarrow{{C}_{1}E}$=λ$\overrightarrow{{C}_{1}C}$(0<λ<1)
如图:在三棱柱ABC-A1B1C1中,∠A1B1C1=90°,A1B1=B1C1=AA1=2,且C在底面A1B1C1上的射影A1C1边的中点,D为AC的中点,点E在CC1上,且$\overrightarrow{{C}_{1}E}$=λ$\overrightarrow{{C}_{1}C}$(0<λ<1)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 归纳推理 | B. | 演绎推理 | C. | 类比推理 | D. | 特殊推理 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com