
分析 (Ⅰ)设任意x1,x2∈[-1,1],且x1<x2,由奇函数的性质化简f(x2)-f(x1),由$\frac{f(a)+f(b)}{a+b}>0$得$\frac{{f({x_2})+f(-{x_1})}}{{{x_2}+(-{x_1})}}>0$,判断出符号后,由函数单调性的定义证明结论成立;
(Ⅱ)根据函数的单调性和定义域列出不等式,求出不等式的解集;
(Ⅲ)由函数的单调性求出f(x)的最大值,由恒成立列出不等式,求出实数m的取值范围.
解答 证明:(Ⅰ)设任意x1,x2∈[-1,1],且x1<x2,
∵f(x)是定义在[-1,1]上的奇函数,
∴f(x2)-f(x1)=f(x2)+f(-x1)
∵x1<x2,∴x2+(-x1)≠0,
由题意知,$\frac{f(a)+f(b)}{a+b}>0$,则$\frac{{f({x_2})+f(-{x_1})}}{{{x_2}+(-{x_1})}}>0$,
∵x2+(-x1)=x2-x1>0,
∴f(x2)+f(-x1)>0,即f(x2)>f(x1),
∴函数f(x)在[-1,1]上是增函数.…(5分)
解:(Ⅱ)由(Ⅰ)和不等式$f(x+\frac{1}{2})<f(1-x)$得,
$\left\{\begin{array}{l}-1≤x+\frac{1}{2}≤1\\-1≤1-x≤1\\ x+\frac{1}{2}<1-x\end{array}\right.$,解得$0≤x<\frac{1}{4}$,
∴不等式的解集是[0,$\frac{1}{4}$)…(9分)
(Ⅲ)由(Ⅰ)得,f(x)最大值为f(1)=1,
所以要使f(x)≤m2-2m+1对所有x∈[-1,1],
只需1≤m2-2m+1恒成立,解得m≤0或m≥2,
得实数m的取值范围为m≤0或m≥2.…(14分)
点评 本题考查定义法证明抽象函数的单调性,奇函数的性质,以及恒成立问题转化为求最值,考查转化思想,化简、变形能力.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
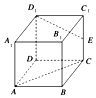 如图所示,在棱长为4的正方体ABCD-A1B1C1D1中,点E是棱CC1的中点,则异面直线D1E与AC所成角的余弦值是$\frac{\sqrt{10}}{5}$.
如图所示,在棱长为4的正方体ABCD-A1B1C1D1中,点E是棱CC1的中点,则异面直线D1E与AC所成角的余弦值是$\frac{\sqrt{10}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2] | B. | (-$\frac{1}{8}$,+∞) | C. | (-2,-$\frac{1}{8}$) | D. | (-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
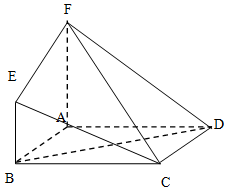 已知空间几何体ABCDEF中,四边形ABCD是正方形,AF⊥平面ABCD,BE⊥平面ABCD,AB=AF=2BE.
已知空间几何体ABCDEF中,四边形ABCD是正方形,AF⊥平面ABCD,BE⊥平面ABCD,AB=AF=2BE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在矩形ABCD中,以DA所在直线为x轴,以DA中点O为坐标原点,建立如图所示的平面直角坐标系.已知点B的坐标为(3,2),E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为⊙H.
在矩形ABCD中,以DA所在直线为x轴,以DA中点O为坐标原点,建立如图所示的平面直角坐标系.已知点B的坐标为(3,2),E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为⊙H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com