
【题目】在某班进行的歌唱比赛中,共有5位选手参加,其中3位女生,2位男生.如果2位男生不能连着出场,且女生甲不能排在第一个,那么出场顺序的排法种数为( )
A. 30B. 36C. 60D. 72
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】f(x)是定义在(0,+∞)上的单调增函数,满足f(xy)=f(x)+f(y),f(3)=1,当f(x)+f(x-8)≤2时,x的取值范围是( )
A.(8,+∞)B.(8,9]C.[8,9]D.(0,8)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂拟生产甲、乙两种适销产品,每件销售收入分别为3000元,2000元.甲、乙产品都需要在A、B两种设备上加工,在每台A、B设备上加工一件甲所需工时分别为1![]() ,2
,2![]() ,加工一件乙设备所需工时分别为2
,加工一件乙设备所需工时分别为2![]() ,1
,1![]() .A、B两种设备每月有效使用台时数分别为400
.A、B两种设备每月有效使用台时数分别为400![]() 和500
和500![]() ,分别用
,分别用![]() 表示计划每月生产甲,乙产品的件数.
表示计划每月生产甲,乙产品的件数.
(Ⅰ)用![]() 列出满足生产条件的数学关系式,并画出相应的平面区域;
列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问分别生产甲、乙两种产品各多少件,可使收入最大?并求出最大收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》(第二季)亮点颇多,十场比赛每场都有一首特别设计的开场诗词,在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《将进酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另确定的两首诗词排在后六场,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后,则后六场的排法有( )
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者A1,A2,A3,A4,A5,A6和4名女志愿者B1,B2,B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.
(I)求接受甲种心理暗示的志愿者中包含A1但不包含![]() 的频率。
的频率。
(II)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,且
,且![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在线段
分别在线段![]() 和
和![]() 上,使四边形
上,使四边形![]() 为正方形,将四边形
为正方形,将四边形![]() 沿
沿![]() 翻折至使
翻折至使![]() .
.
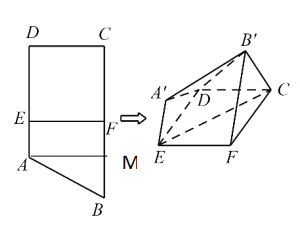
(1)若线段![]() 中点为
中点为![]() ,求翻折后形成的多面体
,求翻折后形成的多面体![]() 的体积;
的体积;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某区组织部为了了解全区科级干部“党风廉政知识”的学习情况,按照分层抽样的方法,从全区320名正科级干部和1280名副科级干部中抽取40名科级干部预测全区科级干部“党风廉政知识”的学习情况.现将这40名科级干部分为正科级干部组和副科级干部组,利用同一份试卷分别进行预测.经过预测后,两组各自将预测成绩统计分析如下表:
分组 | 人数 | 平均成绩 | 标准差 |
正科级干部组 |
| 80 | 6 |
副科级干部组 |
| 70 | 4 |
(1)求![]() ;
;
(2)求这40名科级干部预测成绩的平均分![]() 和标准差
和标准差![]() ;
;
(3)假设该区科级干部的“党风廉政知识”预测成绩服从正态分布![]() ,用样本平均数
,用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() .利用估计值估计:该区科级干部“党风廉政知识”预测成绩小于60分的约为多少人?
.利用估计值估计:该区科级干部“党风廉政知识”预测成绩小于60分的约为多少人?
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ;
;![]() ;
;![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,每次抽奖都是从装有![]() 个红球、
个红球、![]() 个白球的甲箱和装有
个白球的甲箱和装有![]() 个红球、
个红球、![]() 个白球的乙箱中,各随机摸出一个球,在摸出的
个白球的乙箱中,各随机摸出一个球,在摸出的![]() 个球中,若都是红球,则获得一等奖;若只有
个球中,若都是红球,则获得一等奖;若只有![]() 个红球,则获得二等奖;若没有红球,则不获奖.
个红球,则获得二等奖;若没有红球,则不获奖.
(1)求顾客抽奖![]() 次能获奖的概率;
次能获奖的概率;
(2)若某顾客有![]() 次抽奖机会,记该顾客在
次抽奖机会,记该顾客在![]() 次抽奖中获一等奖的次数为
次抽奖中获一等奖的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com