
一空间几何体的三视图如右图所示,该几何体的体积为12π+ ,则正视图与侧视图中x的值为( )
,则正视图与侧视图中x的值为( )
 .
.
 .
.
 .
.
 .
.
C
解析试题分析:几何体是一个组合体,上面是一个正四棱锥,四棱锥的底面是一个对角线为4的正方形,侧棱长是3,下面是一个圆柱,底面直径是4,母线长是x,写出几何体的体积,得到关于x的方程,解出结果.解:由三视图知,几何体是一个组合体,上面是一个正四棱锥,四棱锥的底面是一个对角线为4的正方形,侧棱长是3,根据直角三角形勾股定理知圆锥的高是 下面是一个圆柱,底面直径是4,母线长是x,∵几何体的体积为12π+
下面是一个圆柱,底面直径是4,母线长是x,∵几何体的体积为12π+ ,∴π×4x+
,∴π×4x+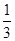 ×(2
×(2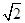 )2×
)2×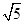 =12π+
=12π+ ∴x=3,故答案为C
∴x=3,故答案为C
考点:由三视图求几何体的体积
点评:本题考查由三视图求几何体的体积,考查由三视图还原几何体,实际上本题不是直接求体积,而是根据体积的值列出关于x的方程,解方程即可


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:单选题
已知三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2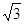 ,AB=1,AC=2,∠BAC=60°,则球O的表面积为
,AB=1,AC=2,∠BAC=60°,则球O的表面积为
A.4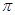 | B.12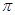 | C.16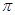 | D.64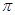 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图所示,在正方体ABCD-A1B1C1D1中,E,F分别为棱AA1,CC1的中点,则在空间中与直线A1D1,EF,CD都相交的直线( ).
| A.有无数条 | B.有且只有两条 | C.有且只有三条 | D.不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
“点动成线,线动成面,面动成体”。如图, 轴上有一条单位长度的线段
轴上有一条单位长度的线段 ,沿着与其垂直的
,沿着与其垂直的 轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形
轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形 ),再把正方形沿着与其所在的平面垂直的
),再把正方形沿着与其所在的平面垂直的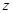 轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体
轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体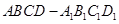 )。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有
)。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有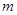 个顶点,
个顶点,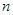 条棱,
条棱, 个面,则
个面,则 的值分别为 ( )
的值分别为 ( )
A. | B.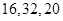 | C.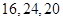 | D.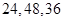 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com