
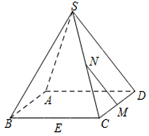
 如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论:
如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论:| A. | ①③ | B. | ③④ | C. | ①② | D. | ②③④ |
分析 如图所示,连接AC、BD相交于点O,连接EM,EN.
(1)由正四棱锥S-ABCD,可得SO⊥底面ABCD,AC⊥BD,进而得到SO⊥AC.可得AC⊥平面SBD.由已知E,M,N分别是BC,CD,SC的中点,利用三角形的中位线可得EM∥BD,MN∥SD,于是平面EMN∥平面SBD,进而得到AC⊥平面EMN,AC⊥EP.
(2)由异面直线的定义可知:EP与BD是异面直线,因此不可能EP∥BD;
(3)由(1)可知:平面EMN∥平面SBD,可得EP∥平面SBD;
(4)由(1)同理可得:EM⊥平面SAC,可用反证法证明:当P与M不重合时,EP与平面SAC不垂直.
解答 解:如图所示,连接AC、BD相交于点O,连接EM,EN.
对于(1),由正四棱锥S-ABCD,可得SO⊥底面ABCD,AC⊥BD,∴SO⊥AC.
∵SO∩BD=O,∴AC⊥平面SBD,∵E,M,N分别是BC,CD,SC的中点,∴EM∥BD,MN∥SD,而EM∩MN=N,
∴平面EMN∥平面SBD,∴AC⊥平面EMN,∴AC⊥EP.故正确.
对于(2),由异面直线的定义可知:EP与BD是异面直线,不可能EP∥BD,因此不正确;
对于(3),由(1)可知:平面EMN∥平面SBD,∴EP∥平面SBD,因此正确.
对于(4),由(1)同理可得:EM⊥平面SAC,若EP⊥平面SAC,则EP∥EM,与EP∩EM=E相矛盾,因此当P与M不重合时,EP与平面SAC不垂直.即不正确.
故选:A.
点评 本题考查了空间线面、面面的位置关系判定,属于中档题.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1:2:1 | B. | 1:2:3 | C. | 2:$\sqrt{3}$:1 | D. | 1:$\sqrt{3}$:2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com