
【题目】从6名短跑运动员中选出4人参加4×100 m接力赛.试求满足下列条件的参赛方案各有多少种?(用数字作答)
(1)甲不能跑第一棒和第四棒;(2)甲不能跑第一棒,乙不能跑第四棒
【答案】(1)240.
(2)252.
【解析】
试题分析:(1)可优先考虑特殊元素甲,此时务必注意甲是否参赛,因此需分两类,甲参赛和甲不参赛,利用分类加法计数原理求解
(2)显然第一、四棒为特殊位置,与之相伴的甲、乙则为特殊元素,这时特殊元素与特殊位置的个数相等,利用特殊位置(元素)优先考虑的原则解之.
(1)优先考虑特殊元素甲,让其选位置,此时务必注意甲是否参赛,因此需分两类:
第1类,甲不参赛有![]() 种排法;
种排法;
第2类,甲参赛,因只有两个位置可供选择,故有A种排法;其余5人占3个位置有A种排法,故有AA种方案.所以有![]() +
+![]()
![]() =240种参赛方案.
=240种参赛方案.
(2)优先考虑特殊位置.
第1类,乙跑第一棒有![]()
![]() =60种排法;
=60种排法;
第2类,乙不跑第一棒有![]()
![]()
![]() =192种排法.
=192种排法.
故共有60+192=252种参赛方案.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=2ax2+(a+4)x+lnx.
(1)若f(x)在x= ![]() 处的切线与直线4x+y=0平行,求a的值;
处的切线与直线4x+y=0平行,求a的值;
(2)讨论函数f(x)的单调区间;
(3)若函数y=f(x)的图象与x轴交于A,B两点,线段AB中点的横坐标为x0 , 证明f′(x0)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某闯关游戏规则是:先后掷两枚骰子,将此试验重复n轮,第n轮的点数分别记为xn , yn , 如果点数满足xn< ![]() ,则认为第n轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束.
,则认为第n轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束.
(Ⅰ)求第一轮闯关成功的概率;
(Ⅱ)如果第i轮闯关成功所获的奖金数f(i)=10000× ![]() (单位:元),求某人闯关获得奖金不超过1250元的概率;
(单位:元),求某人闯关获得奖金不超过1250元的概率;
(Ⅲ)如果游戏只进行到第四轮,第四轮后不论游戏成功与否,都终止游戏,记进行的轮数为随机变量X,求x的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为提高员工的综合素质,聘请专业机构对员工进行专业技术培训,其中培训机构费用成本为12000元.公司每位员工的培训费用按以下方式与该机构结算:若公司参加培训的员工人数不超过30人时,每人的培训费用为850元;若公司参加培训的员工人数多于30人,则给予优惠:每多一人,培训费减少10元.已知该公司最多有60位员工可参加培训,设参加培训的员工人数为![]() 人,每位员工的培训费为
人,每位员工的培训费为![]() 元,培训机构的利润为
元,培训机构的利润为![]() 元.
元.
(1)写出![]() 与
与![]()
![]() 之间的函数关系式;
之间的函数关系式;
(2)当公司参加培训的员工为多少人时,培训机构可获得最大利润?并求最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的短轴长为2,过上顶点E和右焦点F的直线与圆M:x2+y2﹣4x﹣2y+4=0相切.
(a>b>0)的短轴长为2,过上顶点E和右焦点F的直线与圆M:x2+y2﹣4x﹣2y+4=0相切.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l过点(1,0),且与椭圆C交于点A,B,则在x轴上是否存在一点T(t,0)(t≠0),使得不论直线l的斜率如何变化,总有∠OTA=∠OTB (其中O为坐标原点),若存在,求出 t的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某学校准备修建一个面积为2400平方米的矩形活动场地(图中ABCD)的围栏,按照修建要求,中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设![]() 米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
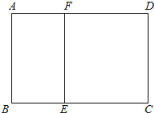
(1)求出y关于x的函数解析式及x的取值范围;
(2)当x为何值时,围墙(包括EF)的修建总费用y最小?并求出y的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数h(x)=lnx+ ![]() .
.
(1)函数g(x)=h(2x+m),若x=1是g(x)的极值点,求m的值并讨论g(x)的单调性;
(2)函数φ(x)=h(x)﹣ ![]() +ax2﹣2x有两个不同的极值点,其极小值为M,试比较2M与﹣3的大小关系,并说明理由.
+ax2﹣2x有两个不同的极值点,其极小值为M,试比较2M与﹣3的大小关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com