
【题目】已知正三角形![]() 的边长为3,
的边长为3,![]() 分别是
分别是![]() 边上的点,满足
边上的点,满足![]() (如图1).将
(如图1).将![]() 折起到
折起到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() ,连接
,连接![]() (如图2).
(如图2).
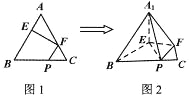
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面与圆O所在的平面互相垂直.已知AB=2,EF=1.
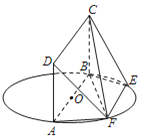
(Ⅰ)求证:平面DAF⊥平面CBF;
(Ⅱ)当AD=1时,求直线FB与平面DFC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)某校夏令营有3名男同学A、B、C和3名女同学X、Y、Z,其年级情况如下表:
一年级 | 二年级 | 三年级 | |
男同学 | A | B | C |
女同学 | X | Y | Z |
现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同).
①用表中字母列举出所有可能的结果;
②设M为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件M发生的概率.
(2)节日前夕,小李在家门前的树上挂了两串彩灯.这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮.那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过2秒的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下三个命题:
①若![]() ,则
,则![]() ;
;
②在![]() 中,若
中,若![]() ,则
,则![]() ;
;
③在一元二次方程![]() 中,若
中,若![]() ,则方程有实数根.
,则方程有实数根.
其中原命题、逆命题、否命题、逆否命题均为真命题的是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4坐标系与参数方程选讲
在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为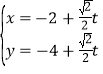 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的平面直角坐标方程和直线
的平面直角坐标方程和直线![]() 的普通方程:
的普通方程:
(2)若![]() 成等比数列,求实数
成等比数列,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某连锁分店销售某种商品,每件商品的成本为4元,并且每件商品需向总店交![]() 元的管理费,预计当每件商品的售价为
元的管理费,预计当每件商品的售价为![]() 元时,一年的销售量为
元时,一年的销售量为![]() 万件.
万件.
(1)求该连锁分店一年的利润![]() (万元)与每件商品的售价
(万元)与每件商品的售价![]() 的函数关系式
的函数关系式![]() ;
;
(2)当每件商品的售价为多少元时,该连锁分店一年的利润![]() 最大,并求出
最大,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为2的菱形![]() 中,
中,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起到
折起到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 平面
平面![]() ,且
,且![]() ,如图2.
,如图2.
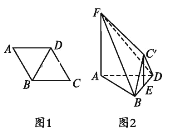
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成角的余弦值;
所成角的余弦值;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照![]() 分成5组,制成如图所示频率分直方图.
分成5组,制成如图所示频率分直方图.
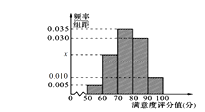
(1)求图中x的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在![]() 内的男生数与女生数3:2,若在满意度评分值为
内的男生数与女生数3:2,若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求2人均为男生的概率.
的人中随机抽取2人进行座谈,求2人均为男生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com