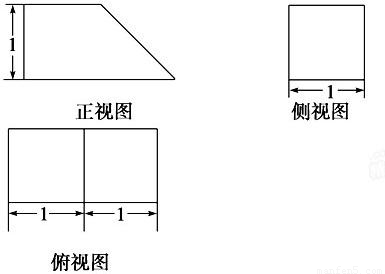
分析:(1)由三视图可知该几何体为棱柱,底面为直角梯形,上下底边长分别为1和2,高为1,侧棱垂直于底面,长为1.由此可画出直观图.
(2)分别求出个面的面积,之和即为表面积;
法一:将该几何体看作一个长方体被截去一个角,而且被截去的部分为一直三棱柱,利用长方体和棱柱的体积公式求解即可.
法二:该几何体为直四棱柱,体面为直角梯形,故利用棱柱的体积公式求解即可.
解答: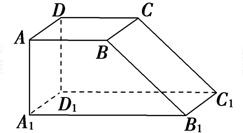
解:(1)由三视图可知该几何体为棱柱,底面为直角梯形,上下底边长分别为1和2,高为1,侧棱垂直于底面,长为1.直观图如图所示:
(2)法一:由三视图可知该几何体是长方体被截去一个角,且该几何体的体积是以A
1A,A
1D
1,A
1B
1为棱的长方体的体积的
,
在直角梯形AA
1B
1B中,作BE⊥A
1B
1于E,则AA
1EB是正方形,
∴AA
1=BE=1.
在Rt△BEB
1中,BE=1,EB
1=1,
∴BB
1=
.
∴几何体的表面积S=S
正方形AA1D1D+2S
梯形AA1B1B+S
矩形BB1C1C+S
正方形ABCD+S
矩形A1B1C1D1=1+2×
×(1+2)×1+1×
+1+1×2
=7+
(m
2).
∴几何体的体积V=
×1×2×1=
(m
3),
∴该几何体的表面积为(7+
)m
2,体积为
m
3.
法二:几何体也可以看作是以AA
1B
1B为底面的直四棱柱,其表面积求法同法一,
V
直四棱柱D1C1CD-A1B1BA=Sh
=
×(1+2)×1×1=
(m
3).
∴几何体的表面积为(7+
)m
2,体积为
m
3.
点评:本题考查空间几何体的三视图、直观图、及几何体的表面积和体积,考查空间想象能力和运算能力.

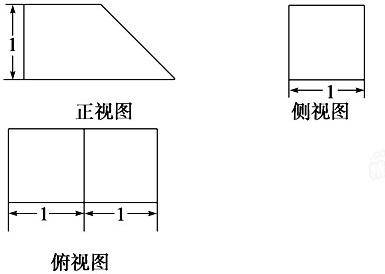 一几何体按比例绘制的三视图如图所示(单位:m)
一几何体按比例绘制的三视图如图所示(单位:m) 解:(1)由三视图可知该几何体为棱柱,底面为直角梯形,上下底边长分别为1和2,高为1,侧棱垂直于底面,长为1.直观图如图所示:
解:(1)由三视图可知该几何体为棱柱,底面为直角梯形,上下底边长分别为1和2,高为1,侧棱垂直于底面,长为1.直观图如图所示: