
【题目】在极坐标系中,曲线C1,C2的极坐标方程分别为ρ=-2cosθ,ρcos![]() =1.
=1.
(1)求曲线C1和C2的公共点的个数;
(2)过极点作动直线与曲线C2相交于点Q,在OQ上取一点P,使|OP|·|OQ|=2,求点P的轨迹,并指出轨迹是什么图形.
【答案】(1)0;(2)![]() 2+
2+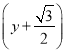 2=1;圆.
2=1;圆.
【解析】
(1)将两个曲线化为普通方程,根据圆心到直线的距离与半径大小进行判定;
(2)用相关点法求解动点的轨迹,利用极坐标进行处理.
(1)C1的直角坐标方程为(x+1)2+y2=1,
它表示圆心为(-1,0),半径为1的圆,
C2的直角坐标方程为x-![]() y-2=0,
y-2=0,
所以曲线C2为直线,
由于圆心到直线的距离为d=![]() >1,
>1,
所以直线与圆相离,即曲线C1和C2没有公共点.
(2)设Q(ρ0,θ0),P(ρ,θ),
![]()
则即![]() ①
①
因为点Q(ρ0,θ0)在曲线C2上,
所以ρ0cos![]() =1,②
=1,②
将①代入②,得![]()
即![]() 为点P的轨迹方程,
为点P的轨迹方程,
化为直角坐标方程为![]() 2+
2+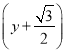 2=1,
2=1,
因此点P的轨迹是以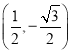 为圆心,1为半径的圆.
为圆心,1为半径的圆.


 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:
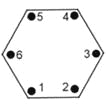
【题目】工人在安装一个正六边形零件时,需要固定如图所示的六个位置的螺丝,第一阶段,首先随意拧一个螺丝,接着拧它对角线上(距离它最远的,下同)螺丝,再随意拧第三个螺丝,第四个也拧它对角线上螺丝,第五个和第六个以此类推,但每个螺丝都不要拧死;第二阶段,将每个螺丝拧死,但不能连续拧相邻的2个螺丝.则不同的固定方式有________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点为极点,x轴的正半轴为极轴建立极坐标系.
(1)试分别将曲线C1的极坐标方程ρ=sinθ-cosθ和曲线C2的参数方程![]() (t为参数)化为直角坐标方程和普通方程;
(t为参数)化为直角坐标方程和普通方程;
(2)若红蚂蚁和黑蚂蚁分别在曲线C1和曲线C2上爬行,求红蚂蚁和黑蚂蚁之间的最大距离(视蚂蚁为点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥P-ABC(如图1)的展开图如图2,其中四边形ABCD为边长等于![]() 的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中.
的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中.
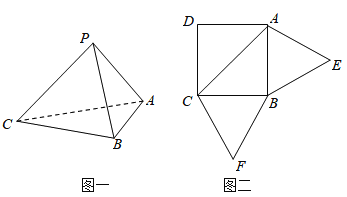
(1)证明:平面PAC⊥平面ABC;
(2)若M,N分别是AP,BC的中点,请判断三棱锥M-BCP和三棱锥N-APC体积的大小关系并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从批量较大的产品中随机取出10件产品进行质量检测,若这批产品的不合格率为0.05,随机变量![]() 表示这10件产品中的不合格产品的件数.
表示这10件产品中的不合格产品的件数.
(1)问:这10件产品中“恰好有2件不合格的概率![]() ”和“恰好有3件不合格的概率
”和“恰好有3件不合格的概率![]() ”哪个大?请说明理由;
”哪个大?请说明理由;
(2)求随机变量![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三个车床加工的零件分别为350个,700个,1050个,现用分层抽样的方法随机抽取6个零件进行检验.
(1)从抽取的6个零件中任意取出2个,已知这两个零件都不是甲车床加工的,求其中至少有一个是乙车床加工的零件;
(2)从抽取的6个零件中任意取出3个,记其中是乙车床加工的件数为X,求X的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com