
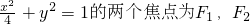 ,点M在椭圆上,
,点M在椭圆上,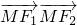 等于-2,则△F1MF2的面积等于
等于-2,则△F1MF2的面积等于

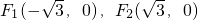 ,从而得到向量
,从而得到向量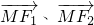 的坐标.设点M坐标为(m,n),根据
的坐标.设点M坐标为(m,n),根据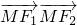 =-2建立关于m、n的一个方程,由点M在椭圆上得到关于m、n的另一个方程,两个方程联解即可得到n=±1,由此结合椭圆的焦距|F1F2|=2
=-2建立关于m、n的一个方程,由点M在椭圆上得到关于m、n的另一个方程,两个方程联解即可得到n=±1,由此结合椭圆的焦距|F1F2|=2 ,即可算出△F1MF2的面积的值.
,即可算出△F1MF2的面积的值. ,
, =
=
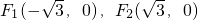
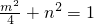 …①
…①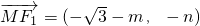 ,
, ,
,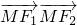 =-2
=-2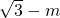 )•(
)•(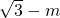 )+(-n)•(-n)=-2,化简得m2+n2=1…②
)+(-n)•(-n)=-2,化简得m2+n2=1…② •|F1F2|•|n|=
•|F1F2|•|n|= ×
× ×1=
×1=
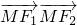 =-2的情况下求△F1MF2的面积,着重考查了平面向量的数量积公式、椭圆的标准方程与简单几何性质等知识点,属于中档题.
=-2的情况下求△F1MF2的面积,着重考查了平面向量的数量积公式、椭圆的标准方程与简单几何性质等知识点,属于中档题. 

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 5 |
| ||
| 6 |
| PF1 |
| PF2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 1 |
| 2 |
| OM |
| 1 |
| 2 |
| OA |
| ||
| 2 |
| OB |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省实验中学高二(上)期末数学试卷(理科)(解析版) 题型:选择题
 ,点M在椭圆上,
,点M在椭圆上,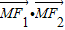 等于-2,则△F1MF2的面积等于( )
等于-2,则△F1MF2的面积等于( )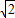
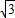
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com