
【题目】根据环境保护部《环境空气质量指数(![]() )技术规定》,空气质量指数(
)技术规定》,空气质量指数(![]() )在201—300之间为重度污染;在301—500之间为严重污染.依据空气质量预报,同时综合考虑空气污染程度和持续时间,将空气重污染分4个预警级别,由轻到重依次为预警四级、预警三级、预警二级、预警一级,分别用蓝、黄、橙、红颜色标示,预警一级(红色)为最高级别.(一)预警四级(蓝色):预测未来1天出现重度污染;(二)预警三级(黄色):预测未来1天出现严重污染或持续3天出现重度污染;(三)预警二级(橙色);预测未来持续3天交替出现重度污染或严重污染;(四)预警一级(红色);预测未来持续3天出现严重污染.
)在201—300之间为重度污染;在301—500之间为严重污染.依据空气质量预报,同时综合考虑空气污染程度和持续时间,将空气重污染分4个预警级别,由轻到重依次为预警四级、预警三级、预警二级、预警一级,分别用蓝、黄、橙、红颜色标示,预警一级(红色)为最高级别.(一)预警四级(蓝色):预测未来1天出现重度污染;(二)预警三级(黄色):预测未来1天出现严重污染或持续3天出现重度污染;(三)预警二级(橙色);预测未来持续3天交替出现重度污染或严重污染;(四)预警一级(红色);预测未来持续3天出现严重污染.
某城市空气质量监测部门对近300天空气中![]() 浓度进行统计,得出这300天
浓度进行统计,得出这300天![]() 浓度的频率分布直方图如图,将
浓度的频率分布直方图如图,将![]() 浓度落入各组的频率视为概率,并假设每天的
浓度落入各组的频率视为概率,并假设每天的![]() 浓度相互独立.
浓度相互独立.
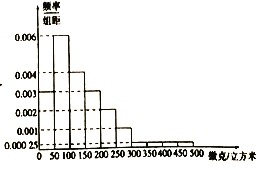
(1)求当地监测部门发布颜色预警的概率;
(2)据当地监测站数据显示未来4天将出现3天严重污染,求监测部门发布红色预警的概率.
【答案】(1)0.2.(2)![]()
【解析】试题分析:(1)观察频率分布直方图,根据题意空气质量指数为重度污染和严重污染的频率为![]() ,所以当地发布颜色预警的概率为0.2;(2 )本问考查古典概型,主要是理解题意并根据题意写出基本事件空间,再根据题中描述预警一级(红色);预测未来持续3天出现严重污染,确定发生红色预警所包含的事件,从而求出概率.
,所以当地发布颜色预警的概率为0.2;(2 )本问考查古典概型,主要是理解题意并根据题意写出基本事件空间,再根据题中描述预警一级(红色);预测未来持续3天出现严重污染,确定发生红色预警所包含的事件,从而求出概率.
试题解析:(1)根据频率分布直方图,可知出现空气重污染的频率是![]() ,所以当地监测部门发布颜色预警的概率是0.2.
,所以当地监测部门发布颜色预警的概率是0.2.
(2)记严重污染为![]() ,其他情况为
,其他情况为![]() ,未来4天中出现3天严重污染的所有情况有
,未来4天中出现3天严重污染的所有情况有![]() ,共4种,发布红色预警所包含的基本事件为
,共4种,发布红色预警所包含的基本事件为![]() ,共2种,所以监测部门发布红色预警的概率
,共2种,所以监测部门发布红色预警的概率![]() .
.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,动圆![]() 与圆
与圆![]() 外切,且与直线
外切,且与直线![]() 相切,记圆心
相切,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设过定点![]() (
(![]() 为非零常数)的动直线
为非零常数)的动直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,问:在曲线
两点,问:在曲线![]() 上是否存在点
上是否存在点![]() (与
(与![]() 两点相异),当直线
两点相异),当直线![]() 的斜率存在时,直线
的斜率存在时,直线![]() 的斜率之和为定值.若存在,求出点
的斜率之和为定值.若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,且
是菱形,且![]() ,点
,点![]() 是棱
是棱![]() 的中点,平面
的中点,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
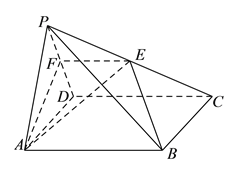
(![]() )求证:
)求证: ![]() .
.
(![]() )若
)若![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
求①二面角![]() 的锐二面角的余弦值.
的锐二面角的余弦值.
②在线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角等于
所成角等于![]() ,若存在,确定
,若存在,确定![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 的
的
部分图像如图所示.
(Ⅰ)求函数![]() 的解析式及
的解析式及![]() 图像的对称轴方程;
图像的对称轴方程;
(Ⅱ)把函数![]() 图像上点的横坐标扩大到原来的
图像上点的横坐标扩大到原来的![]() 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移
![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求关于
的图象,求关于![]() 的方程
的方程![]()
在![]() 时所有的实数根之和.
时所有的实数根之和.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图. 图中A点表示十月的平均最高气温约为![]() ,B点表示四月的平均最低气温约为
,B点表示四月的平均最低气温约为![]() . 下面叙述不正确的是 ( )
. 下面叙述不正确的是 ( )

A. 各月的平均最低气温都在![]() 以上
以上
B. 七月的平均温差比一月的平均温差大
C. 三月和十一月的平均最高气温基本相同
D. 平均最高气温高于![]() 的月份有5个
的月份有5个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为:
的参数方程为: ![]() ,以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为
,以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求直线![]() 和曲线C的普通方程;
和曲线C的普通方程;
(2)在直角坐标系中,过点B(0,1)作直线![]() 的垂线,垂足为H,试以
的垂线,垂足为H,试以![]() 为参数,求动点H轨迹的参数方程,并指出轨迹表示的曲线.
为参数,求动点H轨迹的参数方程,并指出轨迹表示的曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1~4,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1 , S2 , S3 , …,S10 , 则S1+S2+S3+…+S10=
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com