
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且cos2A+cos2B+2sinAsinB=2coc2C. (Ⅰ)求角C的值;
(Ⅱ)若△ABC为锐角三角形,且 ![]() ,求a﹣b的取值范围.
,求a﹣b的取值范围.
【答案】解:(Ⅰ)∵cos2A+cos2B+2sinAsinB=2coc2C, ∴1﹣2sin2A+1﹣2sin2B+2sinAsinB=2(1﹣sin2C),
即sin2C=sin2A+sin2B﹣sinAsinB,
由正弦定理得:c2=a2+b2﹣ab,
∴ ![]() ,
,
且角C角为三角形的内角,即 ![]() .
.
(Ⅱ)由(Ⅰ)知 ![]()
由 ![]() 得,a=2sinA,b=2sinB,
得,a=2sinA,b=2sinB, ![]() ,
,
∵△ABC为锐角三角形, ![]() ,又∵
,又∵ ![]() ,
,
∴A∈( ![]() ,
, ![]() ),
),
∴A﹣ ![]() ∈(﹣
∈(﹣ ![]() ,
, ![]() ),
),
∴ ![]() ,即a﹣b的取值范围为(﹣1,1)
,即a﹣b的取值范围为(﹣1,1)
【解析】(Ⅰ)由已知利用三角函数恒等变换的应用,正弦定理化简已知等式可得c2=a2+b2﹣ab,利用余弦定理可求cosC,结合C角为三角形的内角,可求C的值.(Ⅱ)由(Ⅰ)知 ![]() ,利用正弦定理可求a=2sinA,b=2sinB,利用三角函数恒等变换的应用可求a﹣b=2sin(A﹣
,利用正弦定理可求a=2sinA,b=2sinB,利用三角函数恒等变换的应用可求a﹣b=2sin(A﹣ ![]() ),可求范围A﹣
),可求范围A﹣ ![]() ∈(﹣
∈(﹣ ![]() ,
, ![]() ),利用正弦函数的性质即可得解a﹣b的范围.
),利用正弦函数的性质即可得解a﹣b的范围.
【考点精析】认真审题,首先需要了解正弦定理的定义(正弦定理:![]() ),还要掌握余弦定理的定义(余弦定理:
),还要掌握余弦定理的定义(余弦定理:![]() ;
;![]() ;
;![]() )的相关知识才是答题的关键.
)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={x|x<﹣2或x>0},B={x|( ![]() )x≥3} (Ⅰ)求A∪B
)x≥3} (Ⅰ)求A∪B
(Ⅱ)若集合C={x|a<x≤a+1},且A∩C=C,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p: ![]() <1,q:x2+(a﹣1)x﹣a>0,若p是q的充分不必要条件,则实数a的取值范围是( )
<1,q:x2+(a﹣1)x﹣a>0,若p是q的充分不必要条件,则实数a的取值范围是( )
A.(﹣2,﹣1]
B.[﹣2,﹣1]
C.[﹣3,﹣1]
D.[﹣2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中,其中正确的个数为( ) ①命题“若x2﹣3x+2=0,则x=1”的逆否命题为“若x≠1,则x2﹣3x+2=0”;
②“ ![]() ”是“cos2α=0”的充分不必要条件;
”是“cos2α=0”的充分不必要条件;
③若命题 ![]() ,则p:x∈R,x2+x+1=0;
,则p:x∈R,x2+x+1=0;
④若p∧q为假,p∨q为真,则p,q有且仅有一个是真命题.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知OPQ是半径为 ![]() 圆心角为
圆心角为 ![]() 的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α.
的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α. 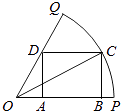
(Ⅰ)若Rt△CBO的周长为 ![]() ,求
,求 ![]() 的值.
的值.
(Ⅱ)求 ![]() 的最大值,并求此时α的值.
的最大值,并求此时α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n和为Sn , 且 ![]() 是
是 ![]() 与(an+1)2的等比中项.
与(an+1)2的等比中项.
(1)求证:数列{an}是等差数列;
(2)若 ![]() ,数列{bn}的前n项和为Tn , 求Tn .
,数列{bn}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为4,P为BC的中点,Q为线段CC1上的动点(异于C点),过点A,P,Q的平面截面记为M.
则当CQ∈时(用区间或集合表示),M为四边形;
当CQ=时(用数值表示),M为等腰梯形;
当CQ=4时,M的面积为 . 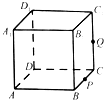
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,A={x| ![]() ≤2x≤8},B={x|x>0},C={x|m<x<m+2}
≤2x≤8},B={x|x>0},C={x|m<x<m+2}
(Ⅰ)求A∩(UB);
(Ⅱ)若A∩C=,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com