
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,左顶点为
,左顶点为![]() ,离心率为
,离心率为![]() ,点
,点![]() 是椭圆上的动点,
是椭圆上的动点,![]() 的面积的最大值为
的面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() ,线段
,线段![]() 的中垂线为
的中垂线为![]() .若直线
.若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,求
,求![]() 的最小值.
的最小值.
 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() ,
,![]() 是抛物线上的两个动点,且
是抛物线上的两个动点,且![]() ,过
,过![]() ,
,![]() 两点分别作抛物线的切线,设其交点为
两点分别作抛物线的切线,设其交点为![]() .
.
(1)若直线![]() 与
与![]() ,
,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,且
,且![]() 的面积为
的面积为![]() ,求
,求![]() 的值;
的值;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大以来,某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领广大农村地区人民群众脱贫奔小康。经过不懈的奋力拼搏,新农村建设取得巨大进步,农民年收入也逐年增加。为了更好的制定2019年关于加快提升农民年收人力争早日脱贫的工作计划,该地扶贫办统计了2018年50位农民的年收人并制成如下频率分布直方图:
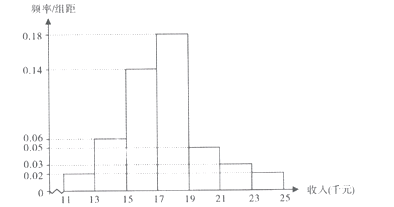
(1)根据频率分布直方图,估计50位农民的年平均收入![]() (单位:千元)(同一组数据用该组数据区间的中点值表示);
(单位:千元)(同一组数据用该组数据区间的中点值表示);
(2)由频率分布直方图,可以认为该贫困地区农民年收入![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为年平均收入
近似为年平均收入![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算得
,经计算得![]() .利用该正态分布,求:
.利用该正态分布,求:
(i)在2019年脱贫攻坚工作中,若使该地区约有占总农民人数的![]() 的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入大约为多少千元?
的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入大约为多少千元?
(ii)为了调研“精准扶贫,不落一人”的政策要求落实情况, 扶贫办随机走访了1000位农民。若每个农民的年收人相互独立,问:这1000位农民中的年收入不少于12.14千元的人数最有可能是多少?
附:参考数据与公式![]() ,若
,若![]() ~
~![]() ,则①
,则①![]() ;②
;②![]() ;③
;③![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z=![]() ,(m∈R,i是虚数单位).
,(m∈R,i是虚数单位).
(1)若z是纯虚数,求m的值;
(2)设![]() 是z的共轭复数,复数
是z的共轭复数,复数![]() +2z在复平面上对应的点在第一象限,求m的取值范围.
+2z在复平面上对应的点在第一象限,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
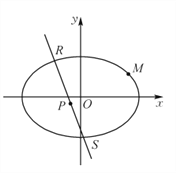
【题目】如图,椭圆![]() 经过点
经过点![]() ,且点
,且点![]() 到椭圆的两焦点的距离之和为
到椭圆的两焦点的距离之和为![]() .
.
(l)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 是椭圆
是椭圆![]() 上的两个点,线段
上的两个点,线段![]() 的中垂线
的中垂线![]() 的斜率为
的斜率为![]() 且直线
且直线![]() 与
与![]() 交于点
交于点![]() ,
,![]() 为坐标原点,求证:
为坐标原点,求证:![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 和曲线
和曲线![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,且两种坐标系中取相同的单位长度.
轴正半轴为极轴,建立极坐标系,且两种坐标系中取相同的单位长度.
(1)求曲线![]() 和曲线
和曲线![]() 的极坐标方程;
的极坐标方程;
(2)设曲线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() ,若射线
,若射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,求
,求![]() 两点间的距离.
两点间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最大值为
的最大值为![]() ,其图像相邻两条对称轴之间的距离为
,其图像相邻两条对称轴之间的距离为![]() ,且
,且![]() 的图像关于点
的图像关于点![]() 对称,则下列判断正确的是()
对称,则下列判断正确的是()
A. 函数![]() 在
在![]() 上单调递增
上单调递增
B. 函数![]() 的图像关于直线
的图像关于直线![]() 对称
对称
C. 当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]()
D. 要得到函数![]() 的图像,只需要
的图像,只需要![]() 将的图像向右平移
将的图像向右平移![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.若数列![]() 、
、![]() 的极限都存在,且
的极限都存在,且![]() ,则数列
,则数列![]() 的极限存在
的极限存在
B.若数列![]() 、
、![]() 的极限都不存在,则数列
的极限都不存在,则数列![]() 的极限也不存在
的极限也不存在
C.若数列![]() 、
、![]() 的极限都存在,则数列
的极限都存在,则数列![]() 、
、![]() 的极限也存在
的极限也存在
D.数![]() ,若数列
,若数列![]() 的极限存在,则数列
的极限存在,则数列![]() 的极限也存在
的极限也存在
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为2的菱形,![]() ,
,![]() 平面ABCD,
平面ABCD,![]() ,且
,且![]() .
.
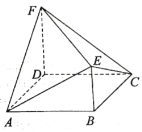
(1)求直线AD和平面AEF所成角的大小;
(2)求二面角E-AF-D的平面角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com