
【题目】在直三棱柱![]() 中,底面为等腰直角三角形,
中,底面为等腰直角三角形, ![]() ,
, ![]() , 若
, 若![]() 、
、![]() 、
、![]() 别是棱
别是棱![]() 、
、![]() 、
、![]() 的中点,则下列四个命题:
的中点,则下列四个命题:
![]() ;
;
②三棱锥![]() 的外接球的表面积为
的外接球的表面积为![]() ;
;
③三棱锥![]() 的体积为
的体积为![]() ;
;
④直线![]() 与平面
与平面![]() 所成角为
所成角为![]()
其中正确的命题有__________.(把所有正确命题的序号填在答题卡上)
【答案】①②③
【解析】根据题意画出如图所示的直三棱柱![]() :
:
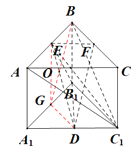
其中,底面为等腰直角三角形, ![]() ,
, ![]() ,
, ![]() 、
、![]() 、
、![]() 别是棱
别是棱![]() 、
、![]() 、
、![]() 的中点.
的中点.
对于①,取![]() 中点
中点![]() ,连接
,连接![]() ,
, ![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
∵![]() 为
为![]() 中点,
中点, ![]() ,
, ![]()
∴四边形![]() 为正方形,则
为正方形,则![]()
在![]() 中,
中, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,则
的中点,则![]() ∥
∥![]() ,且
,且![]() .
.
∵![]() 为
为![]() 的中点,且
的中点,且![]() ∥
∥![]()
∴![]() ∥
∥![]() 且
且![]()
∴四边形![]() 为平行四边形
为平行四边形
∴![]() ∥
∥![]()
∴![]() ,故正确;
,故正确;
对于②,易得![]() ,则
,则![]() .
.
∵![]()
∴![]() ,即
,即![]()
∵![]()
∴三棱锥![]() 的外接球的球心在线段
的外接球的球心在线段![]() 的中点处,则外接球的半径为
的中点处,则外接球的半径为![]()
∴三棱锥![]() 的外接球的表面积为
的外接球的表面积为![]() ,故正确;
,故正确;
对于③,易得![]() ,
, ![]() .
.
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,同理可得
,同理可得![]() ,则三棱锥
,则三棱锥![]() 为正四面体,其体积为
为正四面体,其体积为![]() ,故正确;
,故正确;
对于④,直线![]() 在平面
在平面![]() 上的投影为直线
上的投影为直线![]() ,则
,则![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,在
所成的角,在![]() 中,
中, 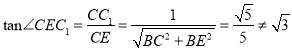 ,故不正确.
,故不正确.
故答案为①②③.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,已知矩形![]() 所在平面垂直于直角梯形
所在平面垂直于直角梯形![]() 所在平面于直线
所在平面于直线![]() ,且
,且![]() ,
, ![]() 且
且![]() ∥
∥![]() .
.
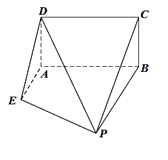
(Ⅰ)设点![]() 为棱
为棱![]() 中点,求证:
中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值等于
所成角的正弦值等于![]() ?若存在,试确定点
?若存在,试确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中点在原点,焦点在
的中点在原点,焦点在![]() 轴上,离心率
轴上,离心率![]() ,以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为
,以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过原点![]() 的两条直线
的两条直线![]() ,
, ![]() ,交椭圆
,交椭圆![]() 于
于![]() ,
, ![]() ,
, ![]() ,
, ![]() 四点,若
四点,若![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),将曲线
为参数),将曲线![]() 上各点的横坐标都缩短为原来的
上各点的横坐标都缩短为原来的![]() 倍,纵坐标坐标都伸长为原来的
倍,纵坐标坐标都伸长为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,在极坐标系(与直角坐标系
,在极坐标系(与直角坐标系![]() 取相同的单位长度,且以原点
取相同的单位长度,且以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市县乡教师流失现象非常严重,为了县乡孩子们能接受良好教育,某市今年要为两所县乡中学招聘储备未来三年的教师,现在每招聘一名教师需要1万元,若三年后教师严重短缺时再招聘,由于各种因素,则每招聘一名教师需要3万元,已知现在该市县乡中学无多余教师,为决策应招聘多少县乡教师搜集并整理了该市50所县乡中学在过去三年内的教师流失数,得到如表的频率分布表:
流失教师数 | 6 | 7 | 8 | 9 |
频数 | 10 | 15 | 15 | 10 |
以这50所县乡中学流失教师数的频率代替一所县乡中学流失教师数发生的概率,记![]() 表示两所县乡中学在过去三年共流失的教师数,
表示两所县乡中学在过去三年共流失的教师数, ![]() 表示今年为两所县乡中学招聘的教师数.为保障县乡孩子教育不受影响,若未来三年内教师有短缺,则第四年马上招聘.
表示今年为两所县乡中学招聘的教师数.为保障县乡孩子教育不受影响,若未来三年内教师有短缺,则第四年马上招聘.
(1)求![]() 的分布列;
的分布列;
(2)若要求![]() ,确定
,确定![]() 的最小值;
的最小值;
(3)以未来四年内招聘教师所需费用的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知鸡的产蛋量与鸡舍的温度有关,为了确定下一个时段鸡舍的控制温度,某企业需要了解鸡舍的温度![]() (单位:
(单位:![]() ),对某种鸡的时段产蛋量
),对某种鸡的时段产蛋量![]() (单位:
(单位:![]() ) 和时段投入成本
) 和时段投入成本![]() (单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度
(单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度![]() 和产蛋量
和产蛋量![]() 的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
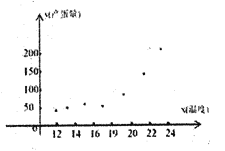
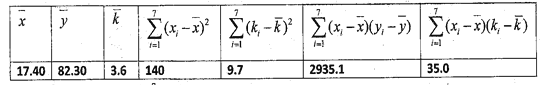
其中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作为该种鸡的时段产蛋量
哪一个更适宜作为该种鸡的时段产蛋量![]() 关于鸡舍时段控制温度
关于鸡舍时段控制温度![]() 的回归方程类型?(给判断即可,不必说明理由)
的回归方程类型?(给判断即可,不必说明理由)
(2)若用![]() 作为回归方程模型,根据表中数据,建立
作为回归方程模型,根据表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知时段投入成本![]() 与
与![]() 的关系为
的关系为![]() ,当时段控制温度为
,当时段控制温度为![]() 时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
附:①对于一组具有线性相关关系的数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为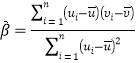 ,
,![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年10月9日,教育部考试中心下发了《关于2017年普通高考考试大纲修订内容的通知》,在各科修订内容中明确提出,增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用.宿州市教育部门积极回应,编辑传统文化教材,在全市范围内开设书法课,经典诵读等课程.为了了解市民对开设传统文化课的态度,教育机构随机抽取了200位市民进行了解,发现支持开展的占![]() ,在抽取的男性市民120人中持支持态度的为80人.
,在抽取的男性市民120人中持支持态度的为80人.
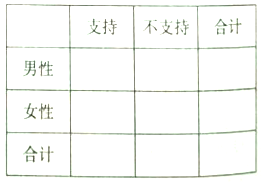
(Ⅰ)完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为性别与支持与否有关?
的把握认为性别与支持与否有关?
(Ⅱ)为了进一步征求对开展传统文化的意见和建议,从抽取的200位市民中对不支持的按照分层抽样的方法抽取5位市民,并从抽取的5人中再随机选取2人进行座谈,求选取的2人恰好为1男1女的概率.
附: 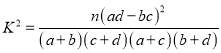 .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com