
分析 (1)易知f(x)=(x-1)3+1,求导f′(x)=3(x-1)2≥0,从而判断;
(2)由题意得(x-1)3+m≥x3-1,即m≥3x2-3x,从而解得.
(3)易知函数f(x)的对称中心为(1,1);从而可得$\frac{1}{1008}$+$\frac{2015}{1008}$=$\frac{2}{1008}$+$\frac{2014}{1008}$=…=2,从而解得.
解答 解:(1)f(1)=(1-1)3+m=m=1,
故f(x)=(x-1)3+1,
f′(x)=3(x-1)2≥0,
故函数f(x)在其定义域R上单调递增;
(2)∵f(x)≥x3-1,∴(x-1)3+m≥x3-1,
即m≥3x2-3x,
∵y=3x2-3x在[1,2]上是增函数,
∴ymin=3-3=0,
∴若关于x的不等式f(x)≥x3-1在区间[1,2]上有解,
则m≥0.
(3)∵f(x)=(x-1)3+1,f′(x)=3(x-1)2,f″(x)=6(x-1);
∴函数f(x)的对称中心为(1,1);
∵$\frac{1}{1008}$+$\frac{2015}{1008}$=$\frac{2}{1008}$+$\frac{2014}{1008}$=…=2,
∴f($\frac{1}{1008}$)+f($\frac{2015}{1008}$)=f($\frac{2}{1008}$)+f($\frac{2014}{1008}$)=…=2,且f($\frac{1008}{1008}$)=f(1)=1,
∴f($\frac{1}{1008}$)+f($\frac{2}{1008}$)+…+f($\frac{2014}{1008}$)+f($\frac{2015}{1008}$)=2×1008-1=2015.
点评 本题考查了导数的综合应用及存在性问题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
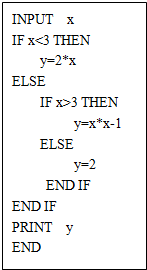
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {-1,1} | C. | ∅ | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\frac{x}{2}$ | B. | f(x)=x+$\frac{1}{2}$ | C. | f(x)=2-x | D. | f(x)=log${\;}_{\frac{1}{2}}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{5}$ | C. | $\frac{11}{5}$ | D. | $\frac{5}{11}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com