函数f(x)=-x(x-a)2(x∈R),
(1)当a>0时,求函数f(x)的极大值和极小值;
(2)当a>3时,求对于任意实数k∈[-1,0],使得不等式f(k-cosx)≥f(k2-cos2x)恒成立的x取值范围.
解:(1)∵f(x)=-x(x-a)
2=-x
3+2ax
2-a
2x,
∴f'(x)=-3x
2+4ax-a
2=-(3x-a)(x-a),
令f'(x)=0,
解得
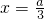
或x=a.…(3分)
∵a>0,∴当x变化时,f'(x)的正负如下表:
…(6分)
因此,函数f(x)在
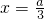
处取得极小值

,且
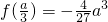
;
函数f(x)在x=a处取得极大值f(a),且f(a)=0.…(8分)
(2)由a>3,得
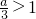
,
当k∈[-1,0]时,k-cosx≤1,k
2-cos
2x≤1.
由(1)知,f(x)在(-∞,1]上是减函数,
要使f(k-cosx)≥f(k
2-cos
2x),
只要k-cosx≤k
2-cos
2x(x∈R),
即cos
2x-cosx≤k
2-k对一切k∈[-1,0]恒成立.
令g(k)=k
2-k,当k∈[-1,0],
g(k)
min=0,
∴cos
2x-cosx≤0,解得0≤cosx≤1,
即
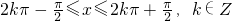
…(12分)
分析:(1)由f(x)=-x(x-a)
2,知f'(x)=-3x
2+4ax-a
2,令f'(x)=0,解得
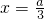
或x=a.列表讨论,能求出函数f(x)的极大值和极小值.
(2)由a>3,得
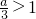
,当k∈[-1,0]时,k-cosx≤1,k
2-cos
2x≤1.由f(x)在(-∞,1]上是减函数,知要使f(k-cosx)≥f(k
2-cos
2x),只要cos
2x-cosx≤k
2-k对一切k∈[-1,0]恒成立.由此能求出使得不等式f(k-cosx)≥f(k
2-cos
2x)恒成立的x取值范围.
点评:本题考查求函数f(x)的极大值和极小值,求对于任意实数k∈[-1,0],使得不等式f(k-cosx)≥f(k
2-cos
2x)恒成立的x取值范围.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.

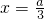 或x=a.…(3分)
或x=a.…(3分)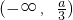

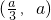
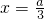 处取得极小值
处取得极小值 ,且
,且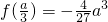 ;
;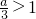 ,
,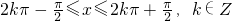 …(12分)
…(12分)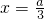 或x=a.列表讨论,能求出函数f(x)的极大值和极小值.
或x=a.列表讨论,能求出函数f(x)的极大值和极小值.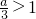 ,当k∈[-1,0]时,k-cosx≤1,k2-cos2x≤1.由f(x)在(-∞,1]上是减函数,知要使f(k-cosx)≥f(k2-cos2x),只要cos2x-cosx≤k2-k对一切k∈[-1,0]恒成立.由此能求出使得不等式f(k-cosx)≥f(k2-cos2x)恒成立的x取值范围.
,当k∈[-1,0]时,k-cosx≤1,k2-cos2x≤1.由f(x)在(-∞,1]上是减函数,知要使f(k-cosx)≥f(k2-cos2x),只要cos2x-cosx≤k2-k对一切k∈[-1,0]恒成立.由此能求出使得不等式f(k-cosx)≥f(k2-cos2x)恒成立的x取值范围.

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案