
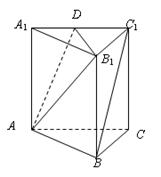
(本小题8分)如图所示,在正三棱柱 中,若
中,若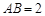 ,
, ,
, 是
是 中点。
中点。
(1)证明: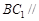 平面
平面 ;
;
(2)求 与
与 所成的角的大小。
所成的角的大小。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013届福建省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
(本小题8分)
如图,点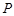 为斜三棱柱
为斜三棱柱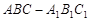 的侧棱
的侧棱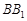 上一点,
上一点,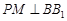 交
交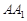 于点
于点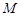 ,
,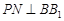 交
交 于点
于点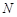 .
.
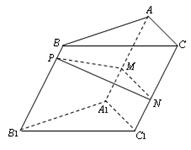
(1) 求证: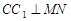 ;
;
(2) 在任意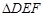 中有余弦定理:
中有余弦定理: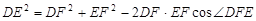 . 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式(只写结论,不必证明)
. 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式(只写结论,不必证明)
查看答案和解析>>
科目:高中数学 来源:2010年浙江省杭州市七校高二上学期期中考试数学理卷 题型:解答题
(本小题8分)
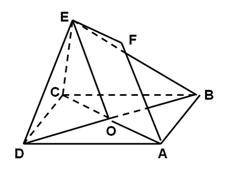
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,EF//AC,AB=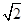 ,CE=EF=1,
,CE=EF=1,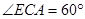 .
.
(1)求证:AF//平面BDE;
(2)求异面直线AB与DE所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2010年浙江省杭州市七校高二上学期期中考试数学文卷 题型:解答题
(本小题8分)
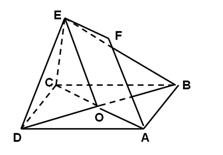
如图,正方形ABCD和四边形ACEF所在的平面互相垂直. EF//AC,AB= ,CE=EF=1,
,CE=EF=1,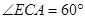 .
.
(1)求证:AF//平面BDE;
(2)求异面直线AB与DE所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题8分)
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,EF//AC,AB=![]() ,CE=EF=1,
,CE=EF=1,![]() .
.
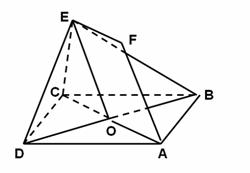 (1)求证:AF//平面BDE;
(1)求证:AF//平面BDE;
(2)求异面直线AB与DE所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com