
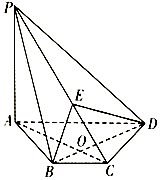
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD交于点O,E为线段PC上的点,且AC⊥BE.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD交于点O,E为线段PC上的点,且AC⊥BE.分析 (1)∵AC⊥BD,AC⊥BE,∴AC⊥平面BDE,∴AC⊥DE.
(2)连接OE,则OE⊥AC,AC⊥AP,∴OE∥AP..∴∠OED(或其补角)就是异面直线ED与PA所成的角.
解△OED即可求异面直线ED与PA所成的角.
解答 解:(1)∵AC⊥BD,AC⊥BE,BD∩BE=E,∴AC⊥平面BDE,∴AC⊥DE.
(2)连接OE,则OE⊥AC,AC⊥AP,∴OE∥AP.∴∠OED(或其补角)就是异面直线ED与PA所成的角.
在等腰梯形ABCD中,计算可得CO=1,OA=2,∴OE=2,又OD=2,且△OED为直角三角形,∴异面直线ED与PA所成的角为45°.
点评 本题考查了线线垂直的判定,异面直线所成的角,考查学生分析解决问题的能力,属于中档题..


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
 如图,已知平面ABC⊥平面BCDE,△DEF与△ABC分别是棱长为1与2的正三角形,AC∥DF,四边形BCDE为直角梯形,DE∥BC,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}(λ∈R,λ>0)$.
如图,已知平面ABC⊥平面BCDE,△DEF与△ABC分别是棱长为1与2的正三角形,AC∥DF,四边形BCDE为直角梯形,DE∥BC,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}(λ∈R,λ>0)$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
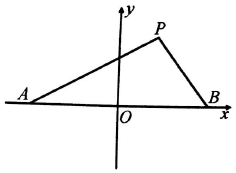 如图,设点A,B的坐标分别为(-$\sqrt{3}$,0),($\sqrt{3}$,0),直线AP,BP相交于点P,且它们的斜率之积为-$\frac{2}{3}$.
如图,设点A,B的坐标分别为(-$\sqrt{3}$,0),($\sqrt{3}$,0),直线AP,BP相交于点P,且它们的斜率之积为-$\frac{2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥2+$\sqrt{3}$ | B. | 0<a<2-$\sqrt{3}$ | C. | a≥2+$\sqrt{3}$或0<a<1 | D. | a≥2+$\sqrt{3}$或0<a<2-$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某程序框图如图所示,若输入输出的n分别为3和1,则在图中空白的判断框中应填入的条件可以为( )
某程序框图如图所示,若输入输出的n分别为3和1,则在图中空白的判断框中应填入的条件可以为( )| A. | i≥7? | B. | i>7? | C. | i≥6? | D. | i<6? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
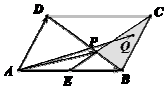 如图,在平行四边形ABCD中,点E为边AB的中点,BD与CE交于点P,若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{AD}(x,y∈R)$,则2x+y=;若点Q是△BCP内部(包括边界)一动点,且$\overrightarrow{AQ}=m\overrightarrow{AB}+n\overrightarrow{AD}(m,n∈R)$,则m+2n的取值范围为[1,3].
如图,在平行四边形ABCD中,点E为边AB的中点,BD与CE交于点P,若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{AD}(x,y∈R)$,则2x+y=;若点Q是△BCP内部(包括边界)一动点,且$\overrightarrow{AQ}=m\overrightarrow{AB}+n\overrightarrow{AD}(m,n∈R)$,则m+2n的取值范围为[1,3].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | 6 | D. | -6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com