
【题目】研究函数f(x)= ![]() 的性质,完成下面两个问题:
的性质,完成下面两个问题:
①将f(2),f(3),f(5)按从小到大排列为;
②函数g(x)= ![]() (x> 0)的最大值为 .
(x> 0)的最大值为 .
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,
, ![]() (
( ![]() 为自然对数的底数).
为自然对数的底数).
(1)设曲线 ![]() 在
在 ![]() 处的切线为
处的切线为 ![]() ,若
,若 ![]() 与点
与点 ![]() 的距离为
的距离为 ![]() ,求
,求 ![]() 的值;
的值;
(2)若对于任意实数 ![]() ,
, ![]() 恒成立,试确定
恒成立,试确定 ![]() 的取值范围;
的取值范围;
(3)当 ![]() 时,函数
时,函数 ![]() 在
在 ![]() 上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系xoy中,直线l的参数方程为 ![]() (t为参数,
(t为参数, ![]() ),以坐标原点o为极点,x轴的正半轴为极轴,并取相同的长度单位,建立极坐标系.曲线
),以坐标原点o为极点,x轴的正半轴为极轴,并取相同的长度单位,建立极坐标系.曲线 ![]()
(1)若直线l曲线 ![]() 相交于点
相交于点 ![]() ,
, ![]() ,
, ![]() ,证明:
,证明: ![]() 为定值;
为定值;
(2)将曲线 ![]() 上的任意点
上的任意点 ![]() 作伸缩变换
作伸缩变换 ![]() 后,得到曲线
后,得到曲线 ![]() 上的点
上的点 ![]() ,求曲线
,求曲线 ![]() 的内接矩形
的内接矩形 ![]() 周长的最大值.
周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设区间D=[﹣3,3],定义在D上的函数f(x)=ax3+bx+1(a>0,b∈R),集合A={a|x∈D,f(x)≥0}.
(1)若b= ![]() ,求集合A;
,求集合A;
(2)设常数b<0 ①讨论f(x)的单调性;
②若b<﹣1,求证:A=.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随机变量 ![]() 的取值为不大于
的取值为不大于 ![]() 的非负整数值,它的分布列为:
的非负整数值,它的分布列为:
| 0 | 1 | 2 |
| n |
|
|
|
|
|
|
其中 ![]() (
( ![]() )满足:
)满足: ![]() ,且
,且 ![]() .
.
定义由 ![]() 生成的函数
生成的函数 ![]() ,令
,令 ![]() .
.
(I)若由 ![]() 生成的函数
生成的函数 ![]() ,求
,求 ![]() 的值;
的值;
(II)求证:随机变量 ![]() 的数学期望
的数学期望 ![]() ,
, ![]() 的方差
的方差 ![]() ;
;
( ![]() )
)
(Ⅲ)现投掷一枚骰子两次,随机变量 ![]() 表示两次掷出的点数之和,此时由
表示两次掷出的点数之和,此时由 ![]() 生成的函数记为
生成的函数记为 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某淘宝商城在2017年前7个月的销售额![]() (单位:万元)的数据如下表,已知
(单位:万元)的数据如下表,已知![]() 与
与![]() 具有较好的线性关系.
具有较好的线性关系. 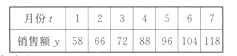
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)分析该淘宝商城2017年前7个月的销售额的变化情况,并预测该商城8月份的销售额.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
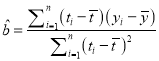 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() 是两个平面,
是两个平面, ![]() 是两条直线,有下列四个命题:
是两条直线,有下列四个命题:
⑴如果 ![]() ,那么
,那么 ![]() .
.
⑵如果 ![]() ,那么
,那么 ![]() .
.
⑶如果 ![]() ,那么
,那么 ![]() .
.
其中正确命题的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x),当x≥0时,f(x)= ![]() ,则关于x的函数F(x)=f(x)﹣a(0<a<1)的所有零点之和为( )
,则关于x的函数F(x)=f(x)﹣a(0<a<1)的所有零点之和为( )
A.3a﹣1
B.1﹣3a
C.3﹣a﹣1
D.1﹣3﹣a
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com