
【题目】已知函数![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 存在最大值
存在最大值![]() ,
, ![]() 存在最小值
存在最小值![]() ,且
,且![]() ,求证:
,求证: ![]() .
.
【答案】(1)![]() 在
在![]() 递增,在
递增,在![]() 递减.(2)证明见解析.
递减.(2)证明见解析.
【解析】试题分析:(1)当求出函数的导数,解关于导函数的不等式,可求出函数的单调区间即可;;(2)求出![]() 的导数,构造函数
的导数,构造函数![]() 求出
求出![]() 的表达式,构造函数
的表达式,构造函数![]() ,根据函数的单调性证出结论.
,根据函数的单调性证出结论.
试题解析:
(1)由题意知, ![]() ,
, ![]() ,
,
![]() 时,
时, ![]() ,
, ![]() 在
在![]() 递减,
递减,
![]() 时,令
时,令![]()
![]() ,令
,令![]()
![]() ,
,
∴![]() 在
在![]() 递增,在
递增,在![]() 递减.
递减.
(2)证明: ![]() ,
,
![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 在
在![]() 递增,无最小值,
递增,无最小值,
由(1)知,此时![]() 无最大值,故
无最大值,故![]() .
.
令![]() ,则
,则![]() ,
,
∵![]() ,
, ![]() ,
,
故存在唯一![]() ,使得
,使得![]() ,即
,即![]() ,
,
列表如下:
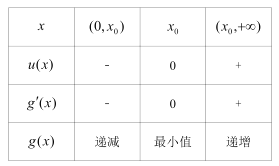
由(1)得:
![]() ,
, ![]() ,
,
由题意![]() ,即
,即![]() ,将
,将![]() 代入上式有:
代入上式有:
![]()
化简得: ![]() (*)
(*)
构造函数![]() ,
, ![]() ,
,
显然![]() 单调递增,且
单调递增,且![]() ,
, ![]() ,
,
则存在唯一![]() ,使得
,使得![]() .
.
且![]() 时,
时, ![]() ,
, ![]() 单调递减;
单调递减; ![]() 时,
时, ![]() ,
, ![]() 单调递增.
单调递增.
又![]() ,故
,故![]() 只会在
只会在![]() 有解,
有解,
而![]()
故(*)的解是![]() ,则
,则![]() .
.


科目:高中数学 来源: 题型:
【题目】统计表明,某种型号的汽车在匀速行驶中每小时耗油量![]() (升)关于行驶速度
(升)关于行驶速度![]() (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: ![]() ,已知甲、乙两地相距100千米.
,已知甲、乙两地相距100千米.
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为![]() 和
和![]() ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:
(1)两种大树各成活1株的概率;
(2)成活的株数ξ的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() 为坐标原点,
为坐标原点, ![]() 是双曲线上在第一象限内的点,直线
是双曲线上在第一象限内的点,直线![]() 分别交双曲线
分别交双曲线![]() 左、右支于另一点
左、右支于另一点![]() ,
, ![]() ,且
,且![]() ,则双曲线
,则双曲线![]() 的离心率为( )
的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(江淮十校2017届高三第一次联考文数试题第7题)《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式为:弧田面积=1/2(弦![]() 矢+矢2).弧田(如图),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为
矢+矢2).弧田(如图),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为![]() ,半径等于4米的弧田.按照上述方法计算出弧田的面积约为( )
,半径等于4米的弧田.按照上述方法计算出弧田的面积约为( )

A. 6平方米 B. 9平方米 C. 12平方米 D. 15平方米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆C:
是椭圆C: ![]() 上一点,点P到椭圆C的两个焦点的距离之和为
上一点,点P到椭圆C的两个焦点的距离之和为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设A,B是椭圆C上异于点P的两点,直线PA与直线![]() 交于点M,
交于点M,
是否存在点A,使得![]() ?若存在,求出点A的坐标;若不存在,请说明理由.
?若存在,求出点A的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com