
分析 (I)由题意可得直线l的方程为:y=x+c,A(x1,y1),B(x2,y2).与椭圆方程联立化为:(a2+b2)x2+2ca2x+a2c2-a2b2=0,利用根与系数的关系代入|AB|=$\sqrt{2[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\frac{4a}{3}$,化简即可得出.
(II)设线段AB的中点M(x0,y0).可得x0=$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{2c}{3}$.y0=x0+c.根据点P(0,-1)满足|PA|=|PB|,可得PM⊥AB,kPM•kAB=-1,解得c.a2=b2+c2=2b2,解得b,a.
解答 解:(I)由题意可得直线l的方程为:y=x+c,A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{y=x+c}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,化为:(a2+b2)x2+2ca2x+a2c2-a2b2=0,
∴x1+x2=-$\frac{2c{a}^{2}}{{a}^{2}+{b}^{2}}$,x1•x2=$\frac{{a}^{2}{c}^{2}-{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$,
|AB|=$\sqrt{2[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{2[\frac{4{c}^{2}{a}^{4}}{({a}^{2}+{b}^{2})^{2}}-\frac{4({a}^{2}{c}^{2}-{a}^{2}{b}^{2})}{{a}^{2}+{b}^{2}}]}$=$\frac{4a}{3}$,
化为:a2=2b2.
∴e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{2}}{2}$.
(II)设线段AB的中点M(x0,y0).
x0=$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{c{a}^{2}}{{a}^{2}+{b}^{2}}$=-$\frac{2c}{3}$.y0=x0+c=$\frac{1}{3}$c.
∵点P(0,-1)满足|PA|=|PB|,∴PM⊥AB,
∴kPM•kAB=$\frac{-1-\frac{1}{3}c}{0+\frac{2c}{3}}$×1=-1,解得c=3.
∴a2=b2+c2=2b2,解得b=c=3,a2=18.
∴椭圆E的方程为$\frac{{x}^{2}}{18}+\frac{{y}^{2}}{9}$=1.
点评 本题考查了椭圆的标准方程及其性质、一元二次方程根与系数的关系、弦长公式、中点坐标公式、相互垂直的直线斜率之间的关系,考查了推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
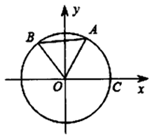 如图,在平面直角坐标系xoy中,A,B,C均为⊙O上的点,其中A($\frac{3}{5}$,$\frac{4}{5}$),C(1,0),点B在第二象限.
如图,在平面直角坐标系xoy中,A,B,C均为⊙O上的点,其中A($\frac{3}{5}$,$\frac{4}{5}$),C(1,0),点B在第二象限.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com