
分析 (1)已知(b2+c2-a2)tanA=$\sqrt{3}$bc,由余弦定理可得:cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{\sqrt{3}}{2tanA}$化简整理即可得出;
(2)利用倍角公式、和差公式可得:f(B)=$sin(2B-\frac{π}{3})$+$\frac{\sqrt{3}}{2}$,0<$C=\frac{2π}{3}-B<\frac{π}{2}$,$0<B<\frac{π}{2}$,可得$\frac{π}{6}<B<\frac{π}{2}$,$(2B-\frac{π}{3})$∈$(0,\frac{2π}{3})$.因此$sin(2B-\frac{π}{3})$∈(0,1],即可得出.
解答 解:(1)∵(b2+c2-a2)tanA=$\sqrt{3}$bc,∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{\sqrt{3}}{2tanA}$,∴sinA=$\frac{\sqrt{3}}{2}$,∵A∈$(0,\frac{π}{2})$,∴$A=\frac{π}{3}$.
(2)∵f(B)=sinBcosB-$\sqrt{3}{cos^2}B+\sqrt{3}$=$\frac{1}{2}sin2B-\sqrt{3}×\frac{1+cosB}{2}$+$\sqrt{3}$=$sin(2B-\frac{π}{3})$+$\frac{\sqrt{3}}{2}$,
∵0<$C=\frac{2π}{3}-B<\frac{π}{2}$,$0<B<\frac{π}{2}$,∴$\frac{π}{6}<B<\frac{π}{2}$,∴$(2B-\frac{π}{3})$∈$(0,\frac{2π}{3})$.
∴$sin(2B-\frac{π}{3})$∈(0,1],
∴f(B)∈$(\frac{\sqrt{3}}{2},1+\frac{\sqrt{3}}{2}]$.
点评 本题考查了余弦定理的应用、和差公式、倍角公式、三角函数的单调性,考查了推理能力与计算能力,属于中档题.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案科目:高中数学 来源: 题型:解答题
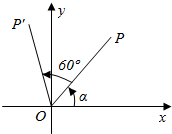 如图,保持点P(3,3)与原点的距离不变,并绕原点旋转60°到P′位置,设点P′的坐标为(x′,y′).
如图,保持点P(3,3)与原点的距离不变,并绕原点旋转60°到P′位置,设点P′的坐标为(x′,y′).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
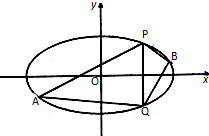 已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{3}}{2}$,它的一个顶点恰好是抛物线x2=4$\sqrt{2}$y的焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{3}}{2}$,它的一个顶点恰好是抛物线x2=4$\sqrt{2}$y的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{13}{6}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com