
 的圆木锯成长方体横梁,横截面为矩形,横梁的强度同它的断面高的平方与宽
的圆木锯成长方体横梁,横截面为矩形,横梁的强度同它的断面高的平方与宽 的积成正比(强度系数为
的积成正比(强度系数为 ,
, ).要将直径为
).要将直径为 的圆木锯成强度最大的横梁,断面的宽
的圆木锯成强度最大的横梁,断面的宽 应是____________
应是____________ 
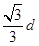
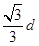 (舍负)。
(舍负)。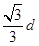 时,f′(x)>0;
时,f′(x)>0;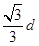 <x<d时,f′(x)<0。
<x<d时,f′(x)<0。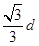 。
。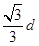 处取最大值,就是横梁强度的最大值。
处取最大值,就是横梁强度的最大值。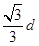 时,横梁的强度最大。
时,横梁的强度最大。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com