
【题目】随着社会的发展,终身学习成为必要,工人知识要更新,学习培训必不可少,现某工厂有工人1000名,其中250名工人参加短期培训(称为![]() 类工人),另外750名工人参加过长期培训(称为
类工人),另外750名工人参加过长期培训(称为![]() 类工人),从该工厂的工人中共抽查了100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)得到
类工人),从该工厂的工人中共抽查了100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)得到![]() 类工人生产能力的茎叶图(左图),
类工人生产能力的茎叶图(左图),![]() 类工人生产能力的频率分布直方图(右图).
类工人生产能力的频率分布直方图(右图).

(1)问![]() 类、
类、![]() 类工人各抽查了多少工人,并求出直方图中的
类工人各抽查了多少工人,并求出直方图中的![]() ;
;
(2)求![]() 类工人生产能力的中位数,并估计
类工人生产能力的中位数,并估计![]() 类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
(3)若规定生产能力在![]() 内为能力优秀,由以上统计数据在答题卡上完成下面的
内为能力优秀,由以上统计数据在答题卡上完成下面的![]() 列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.能力与培训时间列联表
列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.能力与培训时间列联表
短期培训 | 长期培训 | 合计 | |
能力优秀 | |||
能力不优秀 | |||
合计 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
【答案】(1)0.024;(2)可以在犯错误概率不超过![]() 的前提下,认为生产能力与培训时间长短有关
的前提下,认为生产能力与培训时间长短有关
【解析】试题分析:(1)由茎叶图知A类工人中抽查人数为25名,B类工人中应抽查100﹣25=75,由频率分布直方图求出x;
(2)由茎叶图知A类工人生产能力的中位数为122,由(1)及频率分布直方图,估计B类工人生产能力的平均数;
(3)求出K2,与临界值比较,即可得出结论.
试题解析:
解:(1)由茎叶图知A类工人中抽查人数为25名,
∴B类工人中应抽查100-25=75(名).
由频率分布直方图得 (0.008+0.02+0.048+x)10=1,得x=0.024.
(2)由茎叶图知A类工人生产能力的中位数为122
由(1)及频率分布直方图,估计B类工人生产能力的平均数为
![]() 1150.00810+1250.02010+1350.04810+1450.02410=133.8
1150.00810+1250.02010+1350.04810+1450.02410=133.8
(3)由(1)及所给数据得能力与培训的22列联表,
短期培训 | 长期培训 | 合计 | |
能力优秀 | 8 | 54 | 62 |
能力不优秀 | 17 | 21 | 38 |
合计 | 25 | 75 | 100 |
由上表得![]() >10.828
>10.828
因此,可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.

(1)证明: ![]() ;
;
(2)设![]() 为线段
为线段![]() 上的动点,若线段
上的动点,若线段![]() 长的最小值为
长的最小值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)证明线线垂直则需证明线面垂直,根据题意易得![]() ,然后根据等边三角形的性质可得
,然后根据等边三角形的性质可得![]() ,又
,又![]() ,因此
,因此![]() 得
得![]() 平面
平面![]() ,从而得证(2)先找到EH什么时候最短,显然当线段
,从而得证(2)先找到EH什么时候最短,显然当线段![]() 长的最小时,
长的最小时, ![]() ,在
,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,由
,由![]() 中,
中, ![]() ,
, ![]() ,∴
,∴![]() .然后建立空间直角坐标系,写出两个面法向量再根据向量的夹角公式即可得余弦值
.然后建立空间直角坐标系,写出两个面法向量再根据向量的夹角公式即可得余弦值
解析:(1)证明:∵四边形![]() 为菱形,
为菱形, ![]() ,
,
∴![]() 为正三角形.又
为正三角形.又![]() 为
为![]() 的中点,∴
的中点,∴![]() .
.
又![]() ,因此
,因此![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() .
.
而![]() 平面
平面![]() ,
, ![]() 平面
平面![]() 且
且![]() ,
,
∴![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,∴
,∴![]() .
.

(2)如图, ![]() 为
为![]() 上任意一点,连接
上任意一点,连接![]() ,
, ![]() .
.

当线段![]() 长的最小时,
长的最小时, ![]() ,由(1)知
,由(1)知![]() ,
,
∴![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,故
,故![]() .
.
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
由![]() 中,
中, ![]() ,
, ![]() ,∴
,∴![]() .
.
由(1)知![]() ,
, ![]() ,
, ![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,建立如图所示的空间直角坐标系,又
为坐标原点,建立如图所示的空间直角坐标系,又![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,
的中点,
可得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, 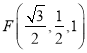 ,
,
所以![]() ,
,  .
.
设平面![]() 的一法向量为
的一法向量为![]() ,
,
则![]() 因此
因此 ,
,
取![]() ,则
,则![]() ,
,
因为![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,
,
故![]() 为平面
为平面![]() 的一法向量.又
的一法向量.又![]() ,
,
所以![]()

![]() .
.
易得二面角![]() 为锐角,故所求二面角的余弦值为
为锐角,故所求二面角的余弦值为![]() .
.

【题型】解答题
【结束】
20
【题目】【2018湖北七市(州)教研协作体3月高三联考】已知椭圆![]() :
: ![]()
![]() 的左顶点为
的左顶点为![]() ,上顶点为
,上顶点为![]() ,直线
,直线![]() 与直线
与直线![]() 垂直,垂足为
垂直,垂足为![]() 点,且点
点,且点![]() 是线段
是线段![]() 的中点.
的中点.

(I)求椭圆![]() 的方程;
的方程;
(II)如图,若直线![]() :
: ![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,点
两点,点![]() 在椭圆
在椭圆![]() 上,且四边形
上,且四边形![]() 为平行四边形,求证:四边形
为平行四边形,求证:四边形![]() 的面积
的面积![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017吉林延边州模拟)已知在△ABC中,B(-1,0),C(1,0),且|AB|+|AC|=4.
(1)求动点A的轨迹M的方程;
(2)P为轨迹M上的动点,△PBC的外接圆为☉O1,当点P在轨迹M上运动时,求点O1到x轴的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着社会的发展,终身学习成为必要,工人知识要更新,学习培训必不可少,现某工厂有工人1000名,其中250名工人参加短期培训(称为![]() 类工人),另外750名工人参加过长期培训(称为
类工人),另外750名工人参加过长期培训(称为![]() 类工人),从该工厂的工人中共抽查了100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)得到
类工人),从该工厂的工人中共抽查了100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)得到![]() 类工人生产能力的茎叶图(左图),
类工人生产能力的茎叶图(左图),![]() 类工人生产能力的频率分布直方图(右图).
类工人生产能力的频率分布直方图(右图).

(1)问![]() 类、
类、![]() 类工人各抽查了多少工人,并求出直方图中的
类工人各抽查了多少工人,并求出直方图中的![]() ;
;
(2)求![]() 类工人生产能力的中位数,并估计
类工人生产能力的中位数,并估计![]() 类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
(3)若规定生产能力在![]() 内为能力优秀,由以上统计数据在答题卡上完成下面的
内为能力优秀,由以上统计数据在答题卡上完成下面的![]() 列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.能力与培训时间列联表
列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.能力与培训时间列联表
短期培训 | 长期培训 | 合计 | |
能力优秀 | |||
能力不优秀 | |||
合计 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于下列四个命题:
p1:x0∈(0,+∞),![]() ;
;
p2:x0∈(0,1),lo![]() x0>lo
x0>lo![]() x0;
x0;
p3:x∈(0,+∞),![]() <lo
<lo![]() x;
x;
p4:x∈![]() <lo
<lo![]() x.
x.
其中的真命题是( )
A. p1,p3 B. p1,p4
C. p2,p3 D. p2,p4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程是
的方程是![]() ,将
,将![]() 向上平移2个单位得到曲线
向上平移2个单位得到曲线![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的参数方程为
的参数方程为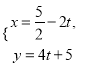 (
(![]() 为参数),判断直线
为参数),判断直线![]() 与曲线
与曲线![]() 的位置关系.
的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正数,Sn是数列{an}的前n项和,且4Sn=an2+2an﹣3.
(1)求数列{an}的通项公式;
(2)已知bn=2n,求Tn=a1b1+a2b2+…+anbn的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com