
【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10![]() cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(1)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(2)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.

【答案】(1)记玻璃棒与![]() 交点为H,则
交点为H,则![]() ,
,![]() ,没入水中的部分为
,没入水中的部分为![]() (cm).
(cm).
(2)![]() ,
,![]() ,
,
记玻璃棒与![]() 交点为Q,则
交点为Q,则
![]() ,∴
,∴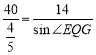 ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,
,
没入水中的部分为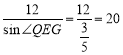 (cm)
(cm)
【解析】
解:(1)由正棱柱的定义,![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,![]() .
.
记玻璃棒的另一端落在![]() 上点
上点![]() 处.
处.
因为![]() ,
,
所以![]() ,从而
,从而 ![]() ,
,
记![]() 与水面的焦点为
与水面的焦点为![]() ,过
,过![]() 作P1Q1⊥AC, Q1为垂足,
作P1Q1⊥AC, Q1为垂足,
则 P1Q1⊥平面 ABCD,故P1Q1=12,
从而 AP1= ![]() .
.
答:玻璃棒l没入水中部分的长度为16cm.
( 如果将“没入水中部分冶理解为“水面以上部分冶,则结果为24cm)
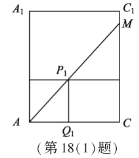
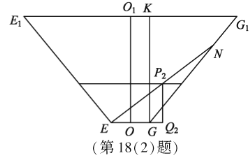
(2)如图,O,O1是正棱台的两底面中心.
由正棱台的定义,OO1⊥平面 EFGH, 所以平面E1EGG1⊥平面EFGH,O1O⊥EG.
同理,平面 E1EGG1⊥平面E1F1G1H1,O1O⊥E1G1.
记玻璃棒的另一端落在GG1上点N处.
过G作GK⊥E1G,K为垂足, 则GK =OO1=32.
因为EG = 14,E1G1= 62,
所以KG1= ![]() ,从而
,从而![]() .
.
设![]() 则
则![]() .
.
因为![]() ,所以
,所以![]() .
.
在![]() 中,由正弦定理可得
中,由正弦定理可得![]() ,解得
,解得![]() .
.
因为![]() ,所以
,所以![]() .
.
于是![]() .
.
记EN与水面的交点为P2,过 P2作P2Q2⊥EG,Q2为垂足,则 P2Q2⊥平面 EFGH,故P2Q2=12,从而 EP2=![]() .
.
答:玻璃棒l没入水中部分的长度为20cm.
(如果将“没入水中部分冶理解为“水面以上部分冶,则结果为20cm)


科目:高中数学 来源: 题型:
【题目】某工厂生产甲、乙两种产品,其产量分别为45个与55个,所用原料分别为A、B两种规格的金属板,每张面积分别为2m2与3m2 . 用A种规格的金属板可造甲种产品3个,乙种产品5个;用B种规格的金属板可造甲、乙两种产品各6个.问A、B两种规格的金属板各取多少张,才能完成计划,并使总的用料面积最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率。
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C![]() 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足![]()
(1) 求点P的轨迹方程;
(2)设点![]() 在直线x=-3上,且
在直线x=-3上,且![]() .证明过点P且垂直于OQ的直线l过C的左焦点F.
.证明过点P且垂直于OQ的直线l过C的左焦点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() sinxcosx+2cos2x﹣1(x∈R) (Ⅰ)求函数f(x)的最小正周期及在区间[0,
sinxcosx+2cos2x﹣1(x∈R) (Ⅰ)求函数f(x)的最小正周期及在区间[0, ![]() ]上的最大值和最小值;
]上的最大值和最小值;
(Ⅱ)若f(x0)= ![]() ,x0∈[
,x0∈[ ![]() ,
, ![]() ],求cos2x0的值.
],求cos2x0的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的偶函数f(x)满足对于任意实数x,都有f(1+x)=f(1﹣x),且当0≤x≤1时,f(x)=3x+1 .
(1)求证:函数f(x)是周期函数;
(2)当x∈[1,3]时,求f(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系内,设M(x1 , y1)、N(x2 , y2)为不同的两点,直线l的方程为ax+by+c=0,设 ![]() .有下列四个说法:
.有下列四个说法:
①存在实数δ,使点N在直线l上;
②若δ=1,则过M、N两点的直线与直线l平行;
③若δ=﹣1,则直线l经过线段MN的中点;
④若δ>1,则点M、N在直线l的同侧,且直线l与线段MN的延长线相交.
上述说法中,所有正确说法的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Sn为公差不为0的等差数列{an}的前n项和,且a1=1,S1 , S2 , S4成等比数列.
(1)求数列{an}的通项公式;
(2)设 ![]() ,求数列{bn}的前n项和.
,求数列{bn}的前n项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com