练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本小题满分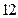分）某学校高三年级有学生1000名，经调查研究,其中750名同学经常参加体育锻炼（称为A类同学），另外250名同学不经常参加体育锻炼(称为B类同学），现用分层抽样方法（按A类、B类分二层）从该年级的学生中共抽查100名同学.
    (Ⅰ)求甲、乙两同学都被抽到的概率，其中甲为A类同学，乙为B类同学；
    (Ⅱ) 测得该年级所抽查的100名同学身高(单位：厘米) 频率分布直方图如右图：
    (ⅰ) 统计方法中，同一组数据常用该组区间的中点值（例如区间的中点值为165）作为代表．据此，计算这100名学生身高数据的期望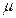及标准差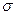(精确到0.1)；
    (ⅱ) 若总体服从正态分布,以样本估计总体,据此,估计该年级身高在范围中的学生的人数．
    (Ⅲ) 如果以身高达170cm作为达标的标准，对抽取的100名学生,得到下列联表:
    体育锻炼与身高达标2×2列联表

     
    		身高达标
    		身高不达标
    		总计
    积极参加体育锻炼
    		40
    		 
    		 
    不积极参加体育锻炼
    		 
    		15
    		 
    总计
    		 
    		 
    		100
    (ⅰ)完成上表；
    (ⅱ)请问有多大的把握认为体育锻炼与身高达标有关系?
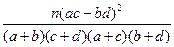    参考公式:K=,参考数据:
    P(Kk)
    		0.40
    		0.25
    		0.15
    		0.10
    		0.05
    		0.025
    k
    		0.708
    		1.323
    		2.072
    		2.706
    		3.841
    		5.024

    （1）1/100（2）=170,（3）（）

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2011届湖南省长沙市第一中学高三第四次月考理科数学试卷 题型：解答题

    （本小题满分13分）某企业的产品以往专销欧美市场，在全球金融风暴的影响下，欧美市场的销量受到严重影响，该企业在政府的大力扶助下积极开拓国内市场，并基本形成了市场规模；自2009年9月以来的第n个月（2009年9月为第一个月）产品的内销量、出口量和销售总量（销售总量=内销量与出口量的和）分别为bn、cn和an(单位：万件)，依据销售统计数据发现形成如下营销趋势：bn + 1 =" a" an，cn + 1 =" an" + b an2 （其中a、b为常数），已知a1 = 1万件，a2 = 1.5万件，a3 = 1.875万件．
    （1）求a，b的值，并写出an + 1与an满足的关系式；
    （2）试用你所学的数学知识论证销售总量逐月递增且控制在2万件内；
    （3）试求从2009年9月份以来的第n个月的销售总量an关于n的表达式．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年辽宁省高三第五次模拟理数试卷（解析版） 题型：解答题

    （本小题满分12分）

    某大学高等数学老师上学期分别采用了两种不同的教学方式对甲、乙两个大一新生班进行教改试验（两个班人数均为60人，入学数学平均分数和优秀率都相同；勤奋程度和自觉性都一样）。现随机抽取甲、乙两班各20名同学的上学期数学期末考试成绩，得到茎叶图如下：

    （Ⅰ）依茎叶图判断哪个班的平均分高？

    （Ⅱ）从乙班这20名同学中随机抽取两名高等数学成绩不得低于85分的同学，求成绩为90分的同学被抽中的概率；

    （Ⅲ）学校规定：成绩不低于85分的为优秀，请填写下面的列联表，并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关？”

     

    甲班

    乙班

    合计

    优秀

     

     

     

    不优秀

     

     

     

    合计

     

     

     

    下面临界值表仅供参考：

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    （参考公式：其中） 

    （Ⅳ）从乙班高等数学成绩不低于85分的同学中抽取2人，成绩不低于90分的同学得奖金100元，否则得奖金50元，记为这2人所得的总奖金，求的分布列和数学期望。

     

    查看答案和解析>>

    科目：高中数学 来源：2014届江西省高二第一次月考理科数学试卷（解析版） 题型：解答题

    （本小题满分１２分）某企业员工500人参加“学雷锋”志愿活动，按年龄分组：第1组[25，30)，第2组[30，35)，第3组[35，40)，第4组[40，45)，第5组[45，50]，得到的频率分布直方图如右图所示．

    (1)下表是年龄的频数分布表，求正整数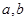的值；

    区间

    [25，30)

    [30，35)

    [35，40)

    [40，45)

    [45，50]

    人数

    50

    50

    150

     

     

     

     

     

    (2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人，年龄在第1,2,3组的人数分别是多少？

    (3)在(2)的前提下，从这6人中随机抽取2人参加社区宣传交流活动，求至少有1人年龄在第3组的概率．

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年山西省太原市高三2月月考文科数学 题型：解答题

    （本小题满分12分）

    为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：

     

    喜爱打篮球

    不喜爱打篮球

    合计

    男生

     

    5

     

    女生

    10

     

    [来源:学|科|网]

    合计

     

     

    50[]

    已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为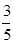

    （1）请将上面的列联表补充完整

    （2）是否有99.5％的把握认为喜爱打篮球与性别有关？说明你的理由；

    （3）已知喜爱打篮球的10位女生中，还喜欢打羽毛球，

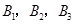
    还喜欢打乒乓球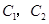，还喜欢踢足球，现在从喜欢打羽毛球、喜欢打乒乓球、

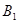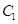    喜欢踢足球的8位女生中各选出1名进行其他方面的调查，求和不全被选

    中的概率．

    下面的临界值表供参考：

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

     

    查看答案和解析>>

    科目：高中数学 来源：北京朝阳区09-10学年高一第二学期期末考试数学试题 题型：解答题

    （本小题满分14分）

    某校高一年级要从3名男生，，和2名女生，中任选3名代表参加学校的演讲比赛.学

    科网          （1）求男生被选中的概率；

      （2）求男生和女生至少一人被选中的概率.

     

    查看答案和解析>>

    同步练习册答案