
| a |
| a |
| b |
| a |
| c |
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| c |


 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源:张家界市一中2007届高三4月模拟考试理科数学试卷 题型:013
下列命题中,正确的个数是
①若|![]() |+|
|+|![]() |=0,则
|=0,则![]() =
=![]() =
=![]() ;②在△ABC中,若
;②在△ABC中,若![]() +
+![]() +
+![]() =
=![]() ,则O为△ABC的重心;
,则O为△ABC的重心;
③若![]() ,
,![]() 是共线向量,则
是共线向量,则![]() ·
·![]() =|
=|![]() |·|
|·|![]() |,反之也成立;
|,反之也成立;
④若![]() ,
,![]() 是非零向量,则
是非零向量,则![]() +
+![]() =
=![]() 的充要条件是存在非零向量
的充要条件是存在非零向量![]() ,使
,使![]() ·
·![]() +
+![]() ·
·![]() =0.
=0.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源:江西省重点中学协作体2012届高三第一次联考数学文科试题 题型:013
若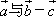 都是非零向量,则“
都是非零向量,则“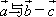 ”是“
”是“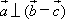 ”的
”的
充分而不必要条件
必要而不充分条件
充分必要条件
既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 |+|
|+| |=0,则
|=0,则 =
= =
= ;
;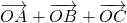 =
= ,则O为△ABC的重心;
,则O为△ABC的重心; ,
, 是共线向量,则
是共线向量,则 •
• =|
=| |•|
|•| |,反之也成立;
|,反之也成立; ,
, 是非零向量,则
是非零向量,则 +
+ =
= 的充要条件是存在非零向量
的充要条件是存在非零向量 ,使
,使 •
• +
+ •
• =
= .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| a |
| a |
| b |
| a |
| c |
| a |
| b |
| c |
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com