Question

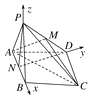
【题目】如图，已知四棱锥P－ABCD，底面ABCD为菱形，且∠DAB＝60°，△PAB是边长为a的正三角形，且平面PAB⊥平面ABCD，已知点M是PD的中点．

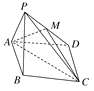
(1)证明：PB∥平面AMC；

(2)求直线BD与平面AMC所成角的正弦值．

Answer 1

【答案】（1）见解析；（2）

【解析】试题分析：（1）连接BD交AC于点O，由三角形中位线可得OM∥PB. 再根据线面平行判定定理得结论（2）先根据空间直角坐标系，再设立各点坐标，根据方程组解得平面法向量，根据向量数量积求向量夹角，最后根据线面角与向量夹角互余关系得结果．

试题解析：(1)证明：连接BD交AC于点O，连接OM，因为四边形ABCD为菱形，OB＝OD，又M为PD的中点，所以OM∥PB.

由PB平面AMC，OM平面AMC，所以PB∥平面ACM.

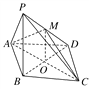
(2)取AB的中点N，连接PN，ND，则∠AND＝90°，

分别以NB，ND，NP为x轴、y轴、z轴建立空间直角坐标系N－xyz，

则B，C，

A，D，P，M，

则＝，＝.

设平面AMC的法向量为n＝(x，y，z)，

则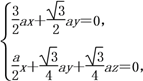令y＝，则x＝－1，

z＝－，即n＝.又＝，设直线BD与n所成的角为θ，则cosθ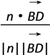＝＝，故直线BD与平面AMC所成角的正弦值为.