
【题目】已知复数z=a2-a-6+![]() i,分别求出满足下列条件的实数a的值:
i,分别求出满足下列条件的实数a的值:
(1)z是实数;
(2)z是虚数;
(3)z是0.
【答案】(1)a=-5或a=3;(2)a≠-5且a≠3且a≠±2;(3)a=3
【解析】
(1)根据题意a2+2a-15=0且a2-4≠0,解得答案.
(2)根据题意a2+2a-15≠0且a2-4≠0,解得答案.
(3)根据题意由a2-a-6=0且a2+2a-15=0,且a2-4≠0,解得答案.
由a2-a-6=0,解得a=-2或a=3.
由a2+2a-15=0,解得a=-5或a=3.
由a2-4≠0,解得a≠±2.
(1)由a2+2a-15=0且a2-4≠0,得a=-5或a=3,
∴当a=-5或a=3时,z为实数.
(2)由a2+2a-15≠0且a2-4≠0,得a≠-5且a≠3且a≠±2,
∴当a≠-5且a≠3且a≠±2时,z是虚数.
(3)由a2-a-6=0且a2+2a-15=0,且a2-4≠0,得a=3,∴当a=3时,z=0.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 与
与![]() 的中心在坐标原点
的中心在坐标原点![]() ,长轴均为
,长轴均为![]() 且在
且在![]() 轴上,短轴长分别为
轴上,短轴长分别为![]() ,
,![]() ,过原点且不与
,过原点且不与![]() 轴重合的直线
轴重合的直线![]() 与
与![]() ,
,![]() 的四个交点按纵坐标从大到小依次为
的四个交点按纵坐标从大到小依次为![]() ,记
,记![]() ,
,![]() 和
和![]() 的面积分别为
的面积分别为![]() 和
和![]() .
.
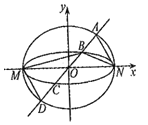
(1)当直线![]() 与
与![]() 轴重合时,若
轴重合时,若![]() ,求
,求![]() 的值;
的值;
(2)当![]() 变化时,是否存在与坐标轴不重合的直线
变化时,是否存在与坐标轴不重合的直线![]() ,使得
,使得![]() ?并说明理由.
?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,
,![]() 单调递增,
单调递增,![]() ,若对任意
,若对任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 是
是![]() 在
在![]() 上的“追逐函数”.若
上的“追逐函数”.若![]() ,则下列四个命题:①
,则下列四个命题:①![]() 是
是![]() 在
在![]() 上的“追逐函数”;②若
上的“追逐函数”;②若![]() 是
是![]() 在
在![]() 上的“追逐函数”,则
上的“追逐函数”,则![]() ;③
;③![]() 是
是![]() 在
在![]() 上的“追逐函数”;④当
上的“追逐函数”;④当![]() 时,存在
时,存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的“追逐函数”.其中正确命题的个数为( )
上的“追逐函数”.其中正确命题的个数为( )
A. ①③B. ②④C. ①④D. ②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=![]() 若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任利用周末时间对该班级![]() 年最后一次月考的语文作文分数进行统计,发现分数都位于
年最后一次月考的语文作文分数进行统计,发现分数都位于![]() 之间,现将所有分数情况分为
之间,现将所有分数情况分为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共七组,其频率分布直方图如图所示,已知
共七组,其频率分布直方图如图所示,已知![]() .
.

(1)求频率分布直方图中![]() 、
、![]() 的值;
的值;
(2)求该班级这次月考语文作文分数的平均数和中位数.(每组数据用该组区间中点值作为代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.


(1)求频率分布直方图中![]() 的值;
的值;
(2)从该小区随机选取一个家庭,试估计这个家庭去年的月均用水量不低于6吨的概率;
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,将该样本看成一个总体,从中任意选取2个家庭,求其中恰有一个家庭的月均用水量不低于8吨的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是![]() 年我国就业人口及劳动年龄人口(劳动年龄人口包含就业人口)统计表:
年我国就业人口及劳动年龄人口(劳动年龄人口包含就业人口)统计表:
时间(年) |
|
|
|
|
|
|
|
就业人口(万人) |
|
|
|
|
|
|
|
劳动年龄人口(万人) |
|
|
|
|
|
|
|
则由表可知( )
A.![]() 年我国就业人口逐年减少
年我国就业人口逐年减少
B.![]() 年我国劳动年龄人口逐年增加
年我国劳动年龄人口逐年增加
C.![]() 年这
年这![]() 年我国就业人口数量的中位数为
年我国就业人口数量的中位数为![]()
D.![]() 年我国劳动年龄人口中就业人口所占比重逐年增加
年我国劳动年龄人口中就业人口所占比重逐年增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆C的标准方程;
(2)点P是椭圆上异于短轴端点A,B的任意一点,过点P作![]() 轴于Q,线段PQ的中点为M.直线AM与直线
轴于Q,线段PQ的中点为M.直线AM与直线![]() 交于点N,D为线段BN的中点,设O为坐标原点,试判断以OD为直径的圆与点M的位置关系.
交于点N,D为线段BN的中点,设O为坐标原点,试判断以OD为直径的圆与点M的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com