考点:数列的求和
专题:点列、递归数列与数学归纳法
分析:(Ⅰ)如果λ=0,根据数列的递推关系即可求数列{a
n}的通项公式;
(Ⅱ)如果λ=2,根据等比数列的定义利用构造法即可证明数列
{an+}为等比数列,并求S
n;
(Ⅲ)求出数列{a
n}的通项公式,利用数列的单调性即可得到结论.
解答:
解:(Ⅰ)λ=0时,S
n=-n,
当n=1时,a
1=S
1=-1,
当n≥2时,a
n=S
n-S
n-1=-1,
所以a
n=-1. …(3分)
(Ⅱ)证明:当λ=2时,S
n=2a
n-
,
S
n+1=2a
n+1-
,
相减得a
n+1=2a
n+
.
所以a
n+1+
=2(a
n+
).
又因为a
1=
,a
1+
=
,
所以数列
{an+}为等比数列,
所以a
n+
=
,S
n=2a
n-
=
-. …(8分)
(Ⅲ)由(Ⅰ)可知,显然λ≠0
当n=1时,则S
1=λa
1-
,得a
1=
.
当n≥2时,S
n=λa
n-
,
S
n-1=λa
n-1-
,
相减得a
n=
a
n-1+
,
即a
n+
=
(a
n-1+
).
因为λ≠±1,所以a
1+
=
≠0.
所以{a
n+
}为等比数列.
所以a
n=
(
)
n-1-
=
(
)
n-
.
因为数列{a
n}为递增数列,
所以
或
,
所以λ的取值范围是λ>1或λ<-1. …(13分)
点评:本题主要考查递推数列的应用,数列的通项公式和前n项和的求解,考查学生的推理和运算能力,综合性较强,运算量较大.



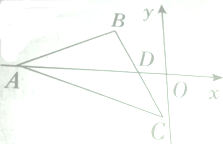 在平面直角坐标系xOy中,A(-4,0)D(-1,0),设△ABC是等腰三角形,点B在x轴上方,且BA=BC,D为BC的中点 若△ABC是正三角形,求直线AB的方程.
在平面直角坐标系xOy中,A(-4,0)D(-1,0),设△ABC是等腰三角形,点B在x轴上方,且BA=BC,D为BC的中点 若△ABC是正三角形,求直线AB的方程.