
分析 通过曲线方程确定曲线表示单位圆在x轴上方的部分(含于x轴的交点),y=$\frac{1}{2}$时,∠AOB=$\frac{2}{3}$π,即可求出扇形AOB的面积.
解答 解:由曲线$τ:\sqrt{1-{x^2}}-y=0$,得x2+y2=1(y≥0)
∴曲线$τ:\sqrt{1-{x^2}}-y=0$表示単位圆在x轴上方的部分(含于x轴的交点)
y=$\frac{1}{2}$时,∠AOB=$\frac{2}{3}$π,扇形AOB的面积为$\frac{1}{2}×\frac{2}{3}π×1×1$=$\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 本题考查直线与圆的位置关系,利用数形结合,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰或直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k=$\frac{1}{e}$+e | |
| B. | 函数f(x)的图象在点(0,f(0))处的切线的斜率为e2-$\frac{1}{e}$ | |
| C. | 函数f(x)在[0,e]上单调递减 | |
| D. | 函数f(x)在[0,e]上的最大值为2e3+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
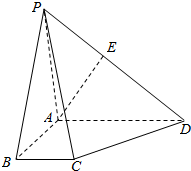 在四棱锥P-ABCD中,底面ABCD是一直角梯形,PA⊥底面ABCD,∠BAD=90°,AD∥BC,AB=BC=1,AD=AP=2,E是PD的中点.
在四棱锥P-ABCD中,底面ABCD是一直角梯形,PA⊥底面ABCD,∠BAD=90°,AD∥BC,AB=BC=1,AD=AP=2,E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com