
【题目】已知正项数列{an}的前n和为Sn , 且 ![]() 是
是 ![]() 与(an+1)2的等比中项.
与(an+1)2的等比中项.
(1)求证:数列{an}是等差数列;
(2)若 ![]() ,数列{bn}的前n项和为Tn , 求Tn .
,数列{bn}的前n项和为Tn , 求Tn .
【答案】
(1)证明:由题意可知, ![]()
当n≥2, ![]()
整理可得(an﹣1)2=(an﹣1+1)2,
∵an>0,
∴an﹣an﹣1=2
n=1,由 ![]()
数列an以1为首项,以2为公差的等差数列
(2)解:由(1)可得an=1+2(n﹣1)=2n﹣1
∴ ![]()
![]() ①
①
![]() ②
②
![]()
∴ ![]()
【解析】(1)要证明数列{an}为等差数列,需证明an﹣an﹣1=d,由已知条件可得 ![]() (2)
(2) ![]() 用错位相减求和
用错位相减求和
【考点精析】通过灵活运用数列的前n项和和等比数列的基本性质,掌握数列{an}的前n项和sn与通项an的关系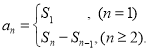 ;{an}为等比数列,则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列即可以解答此题.
;{an}为等比数列,则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列即可以解答此题.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足x2﹣4ax+3a2<0,其中a>0,命题q:实数x满足 ![]() . (Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;
. (Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;
(Ⅱ)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , S3=﹣15,且a1+1,a2+1,a4+1成等比数列,公比不为1.
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且cos2A+cos2B+2sinAsinB=2coc2C. (Ⅰ)求角C的值;
(Ⅱ)若△ABC为锐角三角形,且 ![]() ,求a﹣b的取值范围.
,求a﹣b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣3x+2=0},B={x|x2﹣ax+a﹣1=0},C={x|x2﹣mx+2=0},且A∪B=A,A∩C=C,求实数a,m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.
(I)根据周销量图写出周销量P(件)与单价x(元)之间的函数关系式;
(Ⅱ)写出周利润y(元)与单价x(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.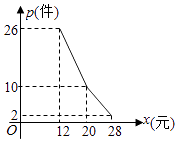
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com